红黑树是一种自平衡二叉搜索树。由于其良好的特性,红黑树被广泛应用于许多地方,例如C++的STL容器以及Linux的非实时任务调度。本文将对红黑树的原理和各种操作算法进行分析。
1 定义
红黑树的示意图如下:
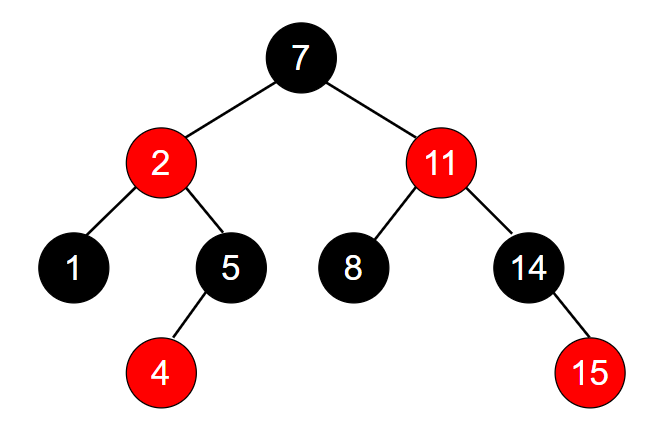
首先,红黑树必须是一棵二叉搜索树。同时,红黑树必须满足以下5条性质:
性质1:每个结点要么是黑色的,要么是红色的;
性质2:根节点必须是黑色的;
性质3:每个“叶子结点”都是黑色的;
容易混淆的是,这里的“叶子结点”并不是我们通常理解的叶结点,而是指空指针结点NIL,所以我们在很多文章中看到的红黑树是下面这个样子的:
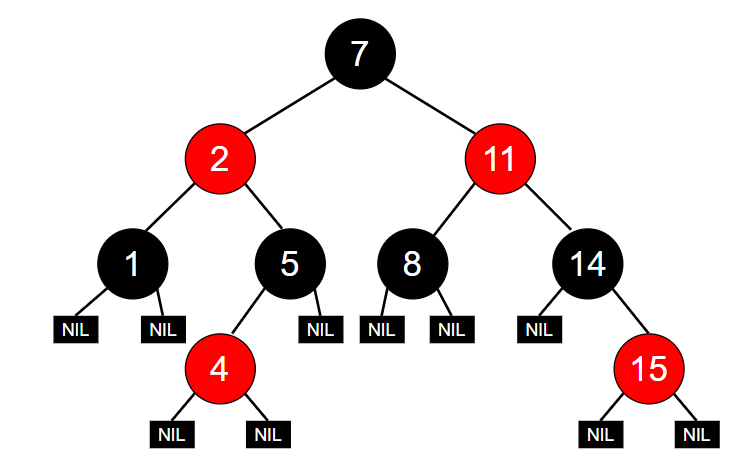
Tips: 个人认为,把NIL结点看做叶子结点非常容易把自己搞晕。。所以这条性质可以理解为这样:如果一个结点的某个子树为空,则假设这个空子树的位置有一个黑色的结点。在后面的红黑树操作分析中,我们可以更好地理解这一条性质。
性质4:如果一个结点是红色的,那么它的两个子结点必须是黑色的;
推论:1. 从任一结点到叶结点的路径上不能出现两个连续的红色结点;2. 红色结点的父结点必须是黑色的。
性质5:对于每个结点,从该结点到子树上叶结点的任意一条路径上,经过的黑色结点数量相同。
这条性质是红黑树最重要的性质,它确保了红黑树中任意一条路径的长度都不会超过其他路径长度的两倍。因此,红黑树是一棵相对接近平衡的二叉树,性能较好。
为了保持这5条性质,我们在插入和删除等操作中需要对红黑树的结构进行相应的调整。
推荐大家看看这个知乎回答:为什么这么多关于红黑树的面试题呢? - 敖丙的回答 - 知乎 https://www.zhihu.com/question/312327402/answer/1560653215
这位大佬比较硬核地解释了红黑树的一些原理,包括2-3-4树模型和红黑树的联系等,看完后会对红黑树有更深的理解!
2 查找 / 搜索
红黑树是一棵二叉搜索树,因此查找操作和普通的二叉搜索树类似,流程如下:
1 | // 搜索值为val的结点 |
3 旋转
在之后对红黑树的结构调整操作中,我们可能需要对某两个结点进行旋转操作,以调节它们的上下关系,使左右子树相对平衡。例如,下面是对结点2进行左旋操作的示意图。注意结点2和结点4的上下关系:
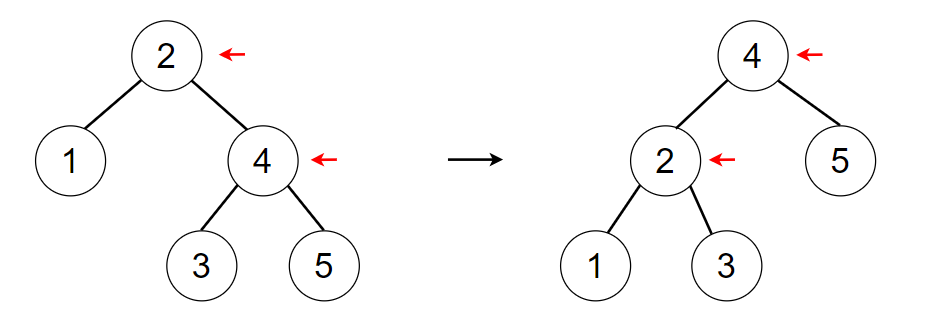
Tips: 刚开始理解旋转操作的时候,有些同学可能会觉得非常抽象,不太明白到底是怎么旋转的。其实我们没必要去关心它究竟是怎么“转”的,因为这些旋转操作都基于一个大前提:这棵树是一棵二叉搜索树。因为旋转只调整两个结点的上下关系,因此在调整好这两个结点后,按照结点值的大小顺序依次将剩余的子树连在对应的位置即可。
以上面的左旋为例,我们需要对结点2进行左旋,因此首先我们调整好结点2和结点4的上下关系,让结点2成为结点4的左子树。由于结点2和结点4的结构关系改变,这两个结点的三个子树(分别为结点1、结点3、结点5)的位置也要相应改变。此时我们只需要根据结点的大小关系,按从小到大的顺序依次插在结点2的左子树、右子树和结点4的右子树。这样一来,从“宏观”上看,该操作看上去就像是将这组结点向左旋转一样。
以此类推,下面是对结点4进行的右旋操作。这里也可以按同样的方式进行理解:
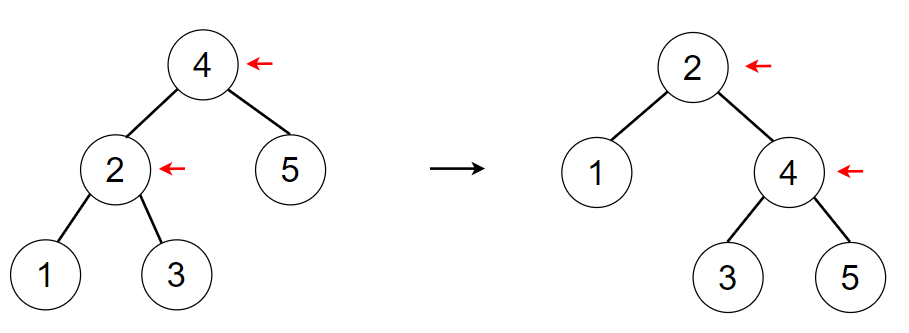
4 插入
4.0 基本思路
- 先将新建的结点插入树中,再调整树的结构
首先,红黑树是一棵二叉搜索树。因此在插入的过程中,我们先按照二叉搜索树的办法将值插入树中。假设插入的值为x,为了后文叙述方便,下图中把与插入的x结点位置相关的几个结点做了命名:
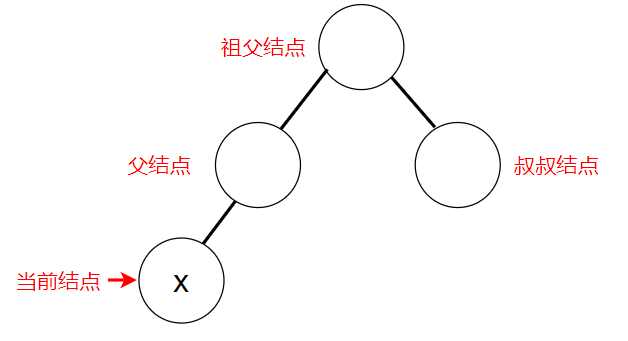
同时,为了满足红黑树的性质,插入结点后我们可能需要对红黑树的结构进行相应的调整。根据目的来分,调整操作总共可以分为两类:调整颜色和调整位置(旋转),具体调整操作根据不同的情况而定。
- 将新插入结点的颜色设为红色
这里回顾一下性质5:对于每个结点,从该结点到子树上叶结点的任意一条路径上,经过的黑色结点数量相同。因此,将新插入的结点设为红色不会破坏性质5的要求。但是插入红色结点后可能会导致其他性质不被满足,这时候再根据下面的不同情况做相应的调整。
另外,下方所有的情况都以插入祖父结点的左子树为例。插入祖父结点的右子树的情况可以镜像地考虑。
4.1 情况1:父结点为黑色
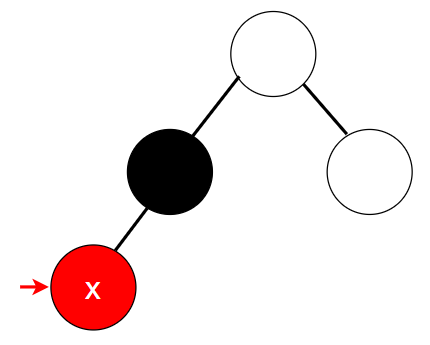
此时不需要对树进行任何调整,插入x结点后红黑树的5条性质都没有被破坏。
4.2 情况2:父结点为红色,且叔叔结点为红色
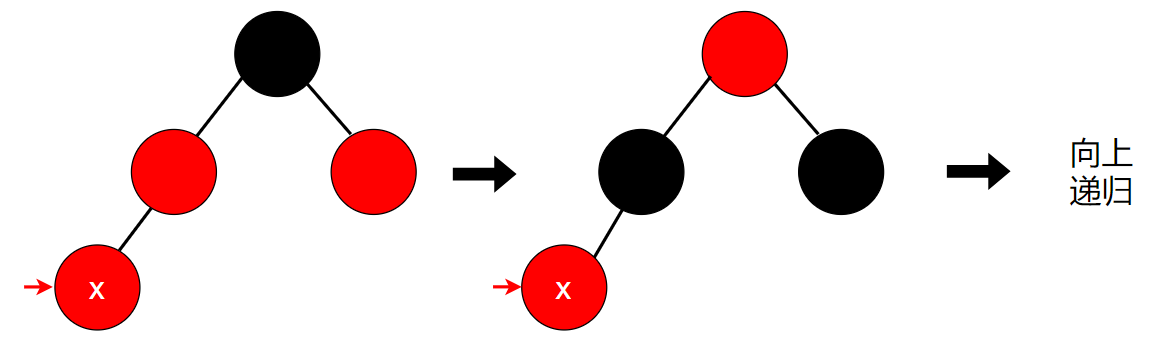
如果父结点为红色,那么祖父结点必定是黑色的。所以这里我们将父结点和叔叔结点都置为黑色,并将祖父结点置为红色,这样一来这组结点就能够满足红黑树的性质。
注意:由于这一操作将祖父结点置成红色,而祖父结点的上方可能还有红色或黑色的结点。因此我们应该递归地向上调整,每次递归结束后将现在的祖父结点当成下一次递归中的当前结点。如果递归到了根结点,无法再继续向上,则将根结点置为黑色并停止递归即可。
4.3 情况3:父结点为红色,且叔叔结点为黑色
4.3.1 当前结点为父结点的右子树
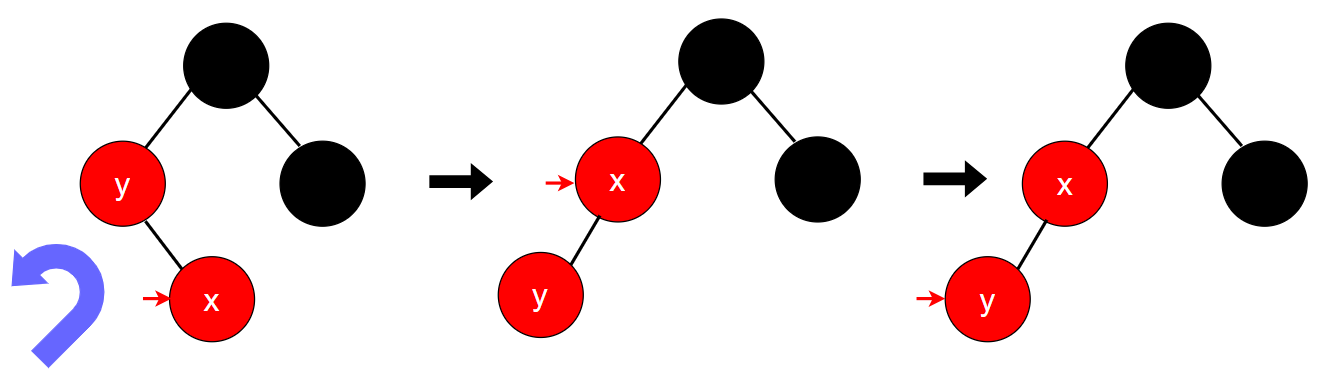
为了方便理解和便于实现,我们尽量考虑插入在父结点左子树上的情况。因此,在父结点y为红色且叔叔结点为黑色的情况下,如果插入的位置是父结点的右子树,我们对父结点做一次左旋操作,并将旋转后的结点y看做当前结点,将旋转后的结点x看做父结点。这样就能转换成后面的插入左子树的情况。
4.3.2 当前结点为父结点的左子树
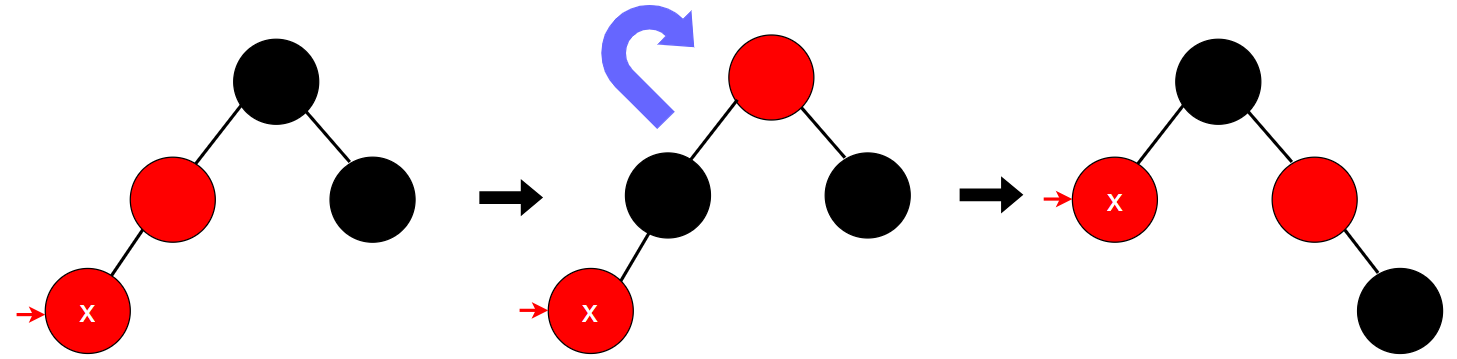
在这种情况下,首先将父结点的颜色和祖父结点的颜色交换,即:将父结点的颜色置为黑色,并将祖父结点置为红色。但这样操作后,从祖父结点向右子树出发,路径上的黑色结点数就会少一个。因此我们对祖父结点做一次右旋操作,将黑色的父结点转到祖父结点的位置,这样右边路径上的黑色结点数量恢复平衡,红黑树的性质满足。
由于调整结束后新的祖父结点的位置仍然是黑色,与调整前相同,因此不需要递归地向上调整。
5 删除
5.0 基本思路
删除操作比插入操作要复杂的多。首先,我们要根据二叉搜索树的删除操作,找到待删除结点所在的位置。之后我们要先将红黑树的结构调整到合适位置,再删除掉目标结点。
类似地,为了叙述便利,假设待删除的值为x,下图中把与当前删除位置相关的几个结点做了命名:
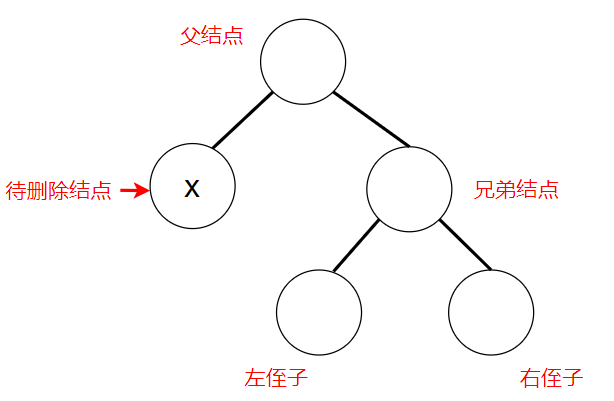
这里我们回顾一下二叉搜索树中删除一个结点的具体操作:
在二叉搜索树中删除值为
x的结点:
- 该结点为叶结点:将该结点的父结点对应的指针置为空指针;
- 该结点的度为1:用该结点唯一的子结点来替换当前结点的位置;
- 该结点的度为2:
- 找到左子树的最大值/右子树的最小值所在的结点,该值记为
m;- 交换找到结点的值
m和待删除结点的值x;- 问题转化为:在子树中删除值为
x的结点。此时目标结点的度一定小于等于1,因此满足上面的两种情况。
而在红黑树中进行删除操作时,需要注意以下几点:
- 只在删除黑色结点时调整
如果删除的结点是红色的,直接删除该结点并不会破坏红黑树的5条性质。因此,待删除的结点为红色时,不需要额外调整树的结构。当待删除的结点是黑色时,需要先调整好红黑树的结构,再将目标结点删除。
- 调整时,想办法使待删除结点的路径上多出1个黑色结点
由于我们只在删除黑色结点的时候才调整结构,而删除黑色结点会导致该条路径上的黑色结点数量减1,因此在调整结构时,我们要想办法使这条路径上多出1个黑色结点,这样调整后我们就可以直接将目标结点删除。
5.1 情况1:兄弟结点为红色
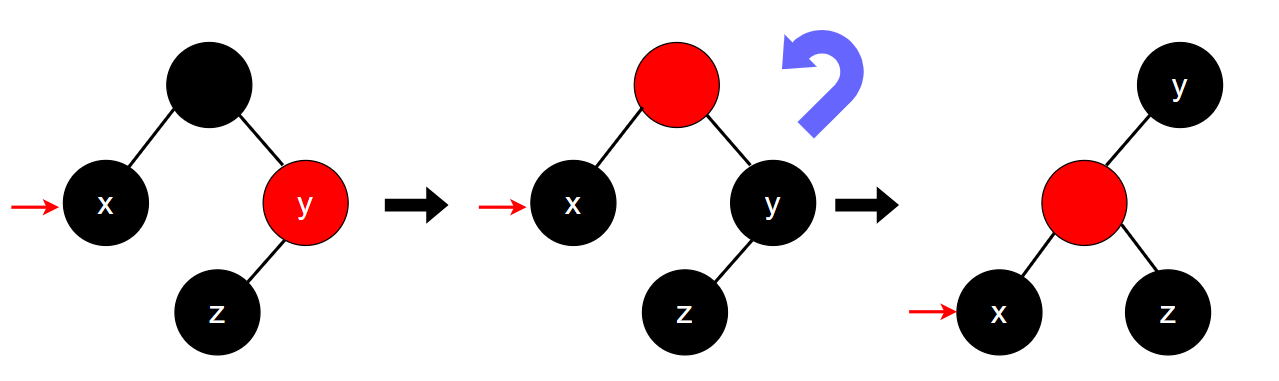
当兄弟结点为红色时,我们总能通过下面这一系列操作将其调整为兄弟结点为黑色的情况,从而满足后文叙述的三种情形之一。
- 调整颜色
- 将兄弟结点的颜色和父结点的颜色交换,即:将父结点置为红色,并将兄弟结点置为黑色;
- 调整位置
- 对父结点进行左旋
操作结束后,x结点的新的兄弟结点就变为黑色的了。然而,到这里调整操作并没有结束。我们需要继续判断当前的x结点符合下列三种情况的哪一种,并进行后续操作。
5.2 情况2:兄弟为黑色,右侄子为红色,左侄子任意
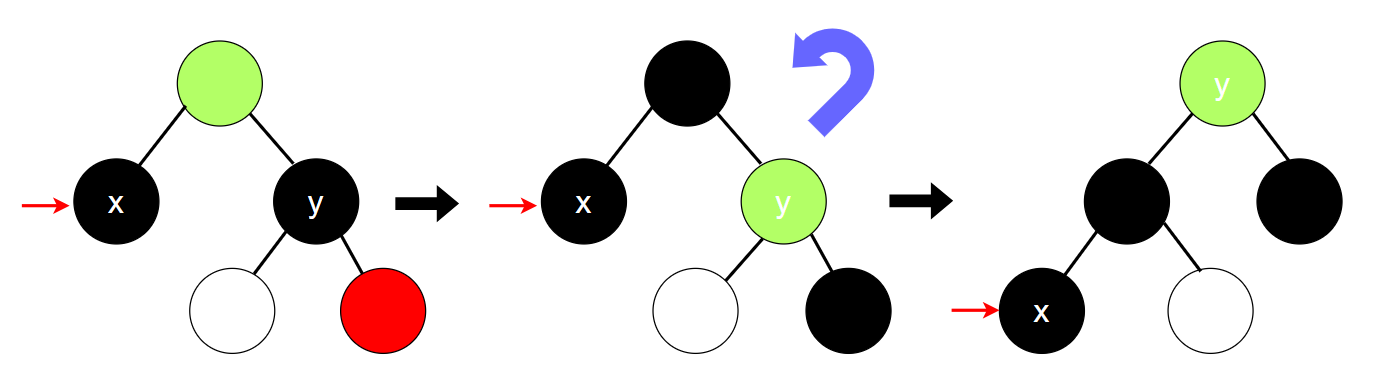
当兄弟结点为黑色时,我们应该首先关注右侄子的情况。
如果右侄子为红色,那么不管左侄子是什么颜色,我们都可以通过下面的步骤完成调整操作:
调整颜色
- 交换兄弟结点和父结点的颜色(父结点颜色任意,图中用绿色表示),即:将兄弟结点置为父结点的颜色,并将父结点置为黑色;
- 将右侄子置为黑色;
- 调整颜色后,左右子树的路径上都会多出1个黑色的结点;
调整位置
- 对父结点进行左旋;
- 这样左边的黑色结点仍然多出1个,而右边的黑色结点个数与之前相同。
调整完成后,将待删除结点删除即可。
5.3 情况3:兄弟为黑色,右侄子为黑色,左侄子为红色
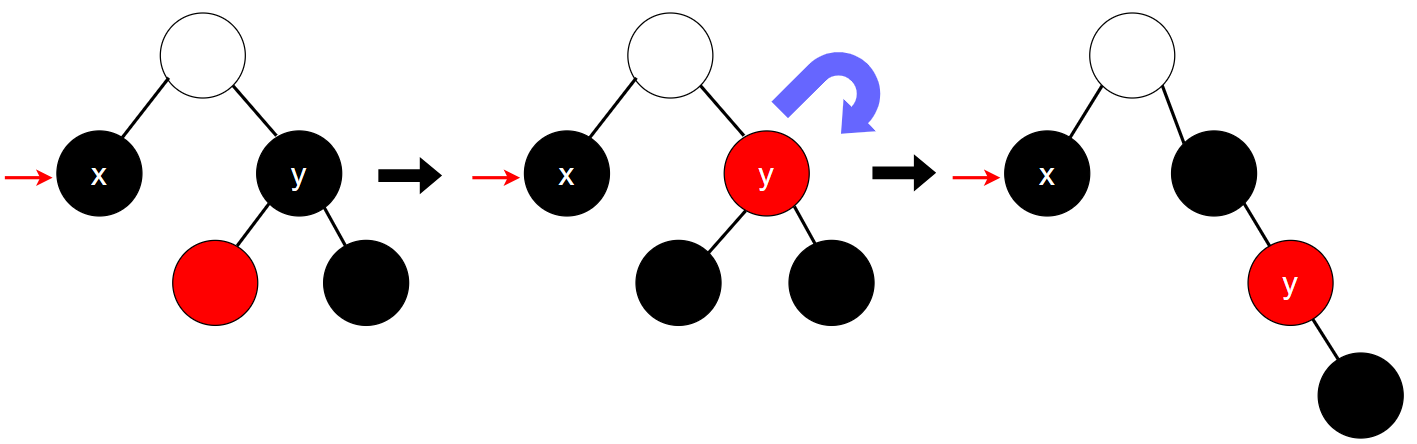
这种情况可以通过以下步骤转化为情况2:
- 调整颜色
- 将兄弟结点的颜色和左侄子的颜色交换,即:将兄弟结点置为红色,并将左侄子置为黑色;
- 调整位置
- 对兄弟结点进行右旋。
调整结束后,待删除结点的兄弟结点为黑色,并且右侄子为红色,因此进入情况2进行后续操作。
5.4 情况4:兄弟为黑色,右侄子为黑色,左侄子为黑色
5.4.1 父结点为红色
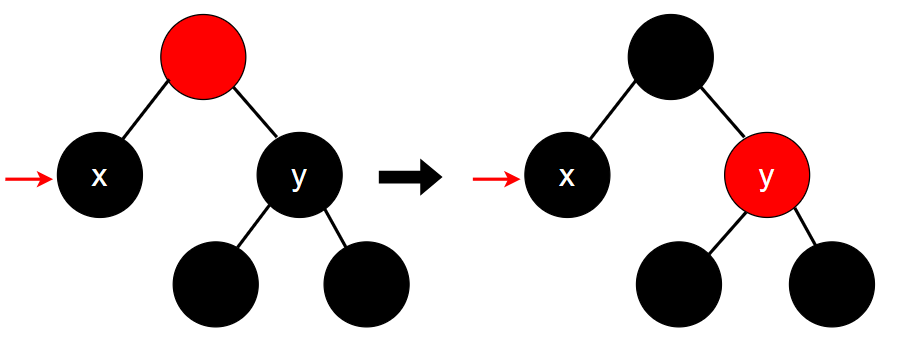
当父结点为红色时,只需要交换兄弟结点和父结点的颜色即可。即:将父结点置为黑色,并将兄弟结点置为红色。此时,右边路径的黑色结点数不变,而左边路径的黑色结点数多出了1个。
调整完成后,将待删除结点删除即可。
5.4.2 父结点为黑色
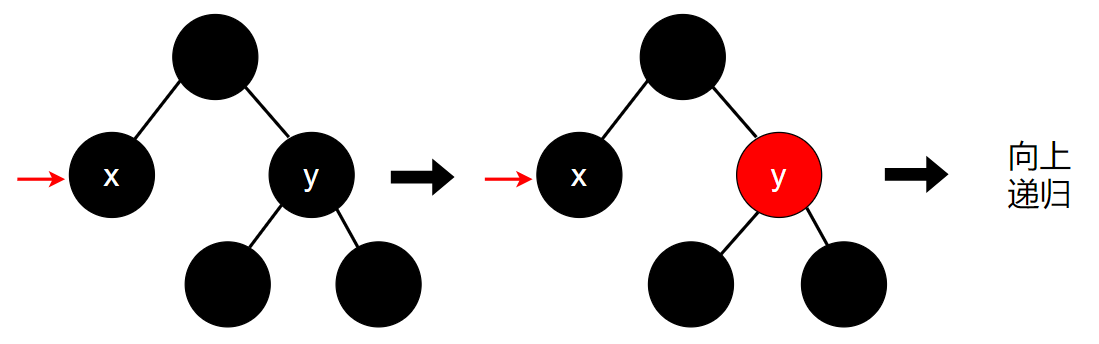
当父结点为黑色时,首先我们将兄弟结点的颜色置为红色。这样一来,右边的路径上黑色结点的个数就比原来少了1个,而左边路径上黑色结点的个数和原来一样。
但是我们的目标是:让左边路径上的黑色结点个数比原来多1个,而右边路径上和原来一样。也就是说,这样调整之后,左右两条路径的黑色结点个数都比预期少了一个。因此我们期待父结点上方的结构能够调整一下,让父结点上方的路径多出一个黑色结点来。
所以在调整完兄弟结点的颜色后,我们递归地向上继续调整红黑树的结构,将当前的父结点当做下一次递归中的待删除结点。如果递归到了根结点,无法再继续向上,则停止递归即可。
下一篇文章(红黑树的 C++ 实现)将介绍如何用C++来实现一个基本的红黑树数据结构。