算法设计与分析 - 分治法

1 简介

• 流程：divide → conquer(recursive) → combine
• 关键问题
  • 如何划分为子问题
  • 如何解决递归尾部的最小原子问题
  • 如何将各子部分结合起来

1.1 例子

• 复数相乘：(a + bi)(c + di) = ac - bd + (ad + bc)i
• 优化：ad + bc = (a + c)(b + d) - ac - bd
• 这样可以将4个乘法优化到3个乘法

1.2 使用上例优化整数乘法

设有两个n位二进制整数x、y，将整数分成高位、低位两部分

• 该算法的运行时间为 $T(n) = 4T(n / 2) + O(n)$
  • 使用后面提到的主定理分析，复杂度为 $O(n^2)$
• 利用1.1的优化方案，运行时间为 $T(n) = 3T(n / 2) + O(n)$
  • 使用主定理，复杂度为 $O(n^{log_23}) \approx O(n^{1.58})$

2 主定理

$T(n) = a T(\lceil n / b \rceil) + O(n^d)$

• $O(n^d)$：merge消耗的复杂度 $T(n) = a T(\lceil n / b \rceil) + O(n^d)$
• b：每次分成b段
• a：每次在分好的b段中使用几段
  • a可以小于b，如二分搜索a = 1，b = 2
  • a可以大于b，当使用的子问题有overlap的时候

结论：

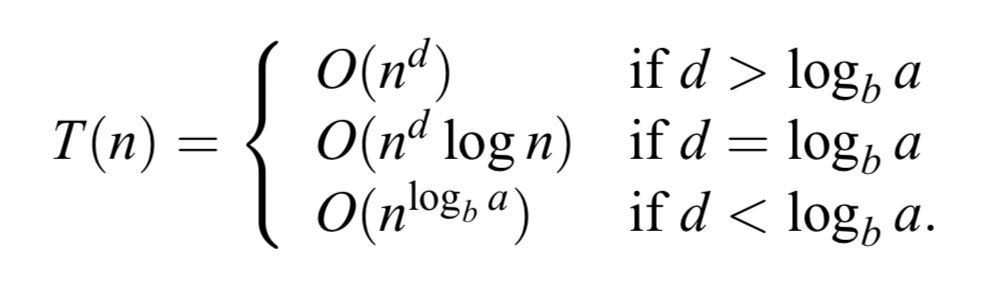
Tips：比较 a 和 $b^d$

证明：

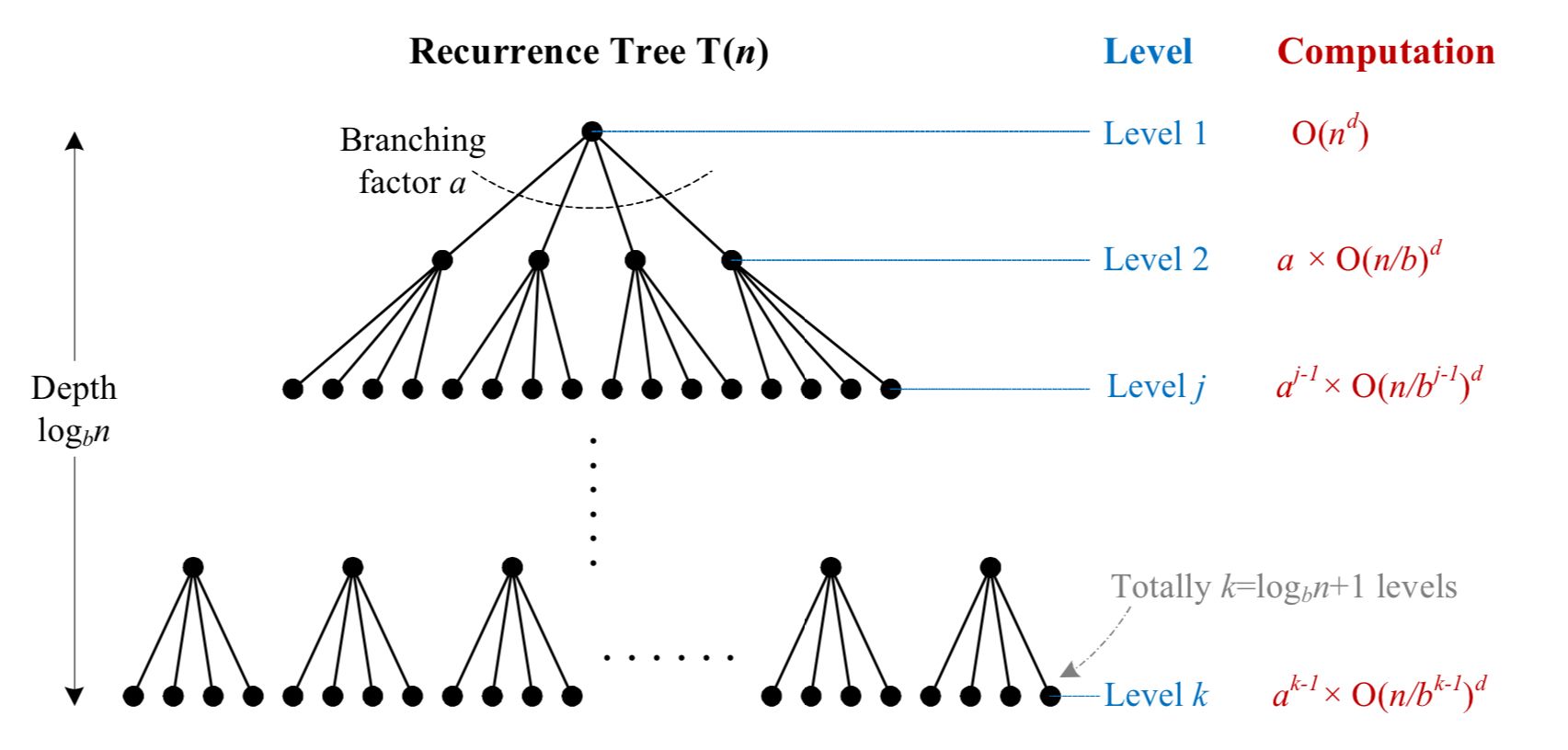
→ $T(n) = O(n^d) \sum_{j=0}^{log_bn} (\frac{a}{b^d})^j$

• $\frac{a}{b^d} = 1$
  • $T(n) = O(n^d) \cdot log_bn = O(n^dlogn)$
• $\frac{a}{b^d} < 1$
  • 等比求和
  • $T(n) = O(n^d) \cdot \frac{1}{1 - \frac{a}{b^d}} = O(n^d)$
• $\frac{a}{b^d} > 1$
  • 等比求和
  • $T(n) = O(n^d) \cdot \frac{(\frac{a}{b^d})^{log_bn}}{1 - \frac{a}{b^d}} = O(n^d \cdot \frac{a^{log_bn}}{n^d})=O(a^{log_bn})=O(n^{log_ba})$

3 排序算法的下界

由permutation tree可知：叶结点共有n!个

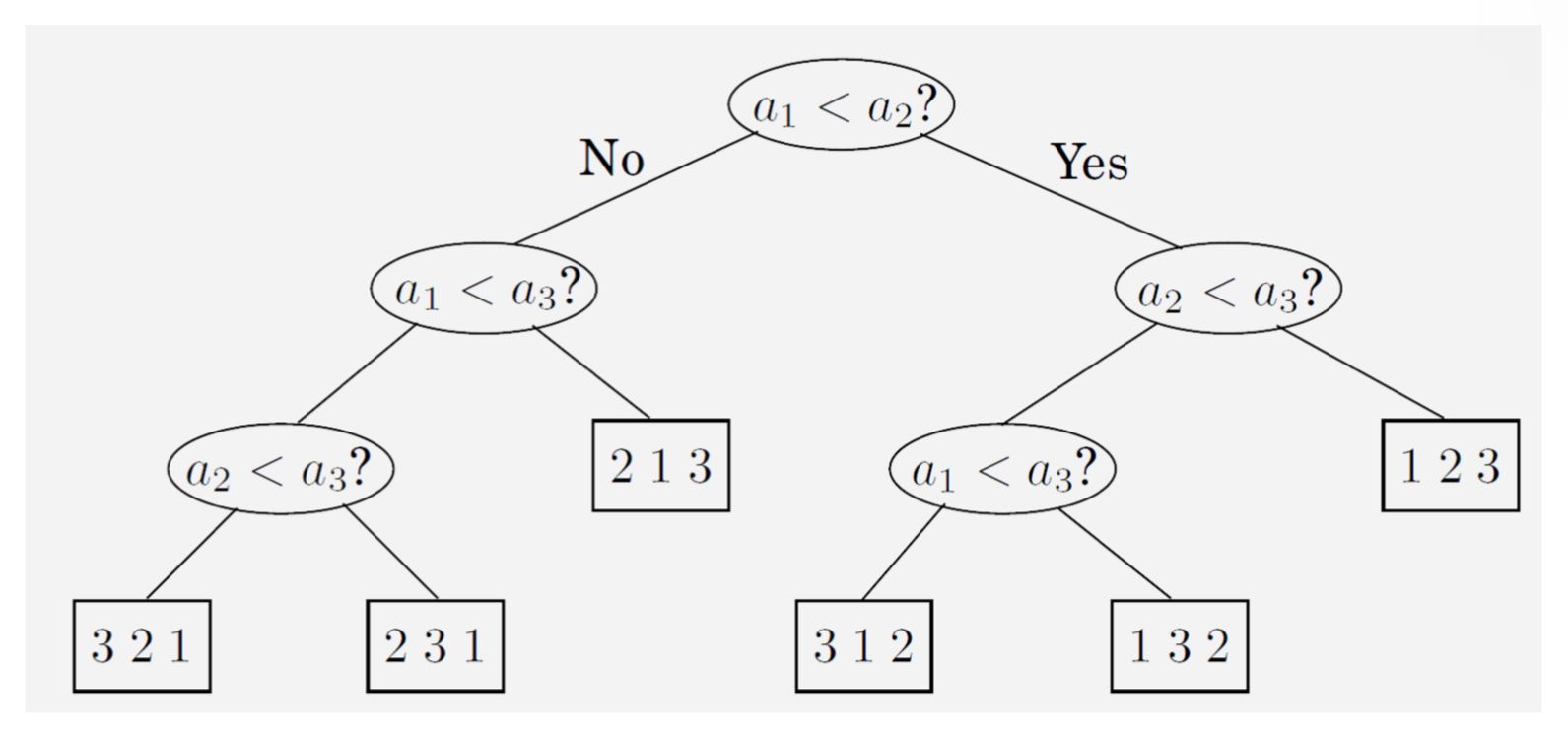
因此，排序算法的复杂度至少为 $\Omega(log(n!)) = \Omega(nlogn)$

重要结论： $log(n!) = \Theta(nlogn)$ 证明：两边夹

$$\begin{align*} (\frac{n}{2})^{\frac{n}{2}} \le n! \le n^n &\Rightarrow \frac{n}{2} \log \frac{n}{2} \le \log(n!) \le n\log n \\ &\Rightarrow \Theta(n \log n) \le \log(n!) \le \Theta(n \log n) \end{align*}$$

4 矩阵乘法的复杂度

• 普通矩阵乘法： $O(n^3)$

• 普通拆分方法

  

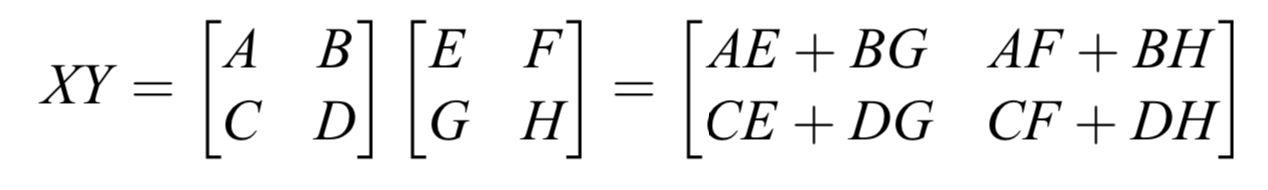
• $T(n) = 8T(n / 2) + O(n^2)$ → 复杂度 $O(n^3)$

• 优化方法

  

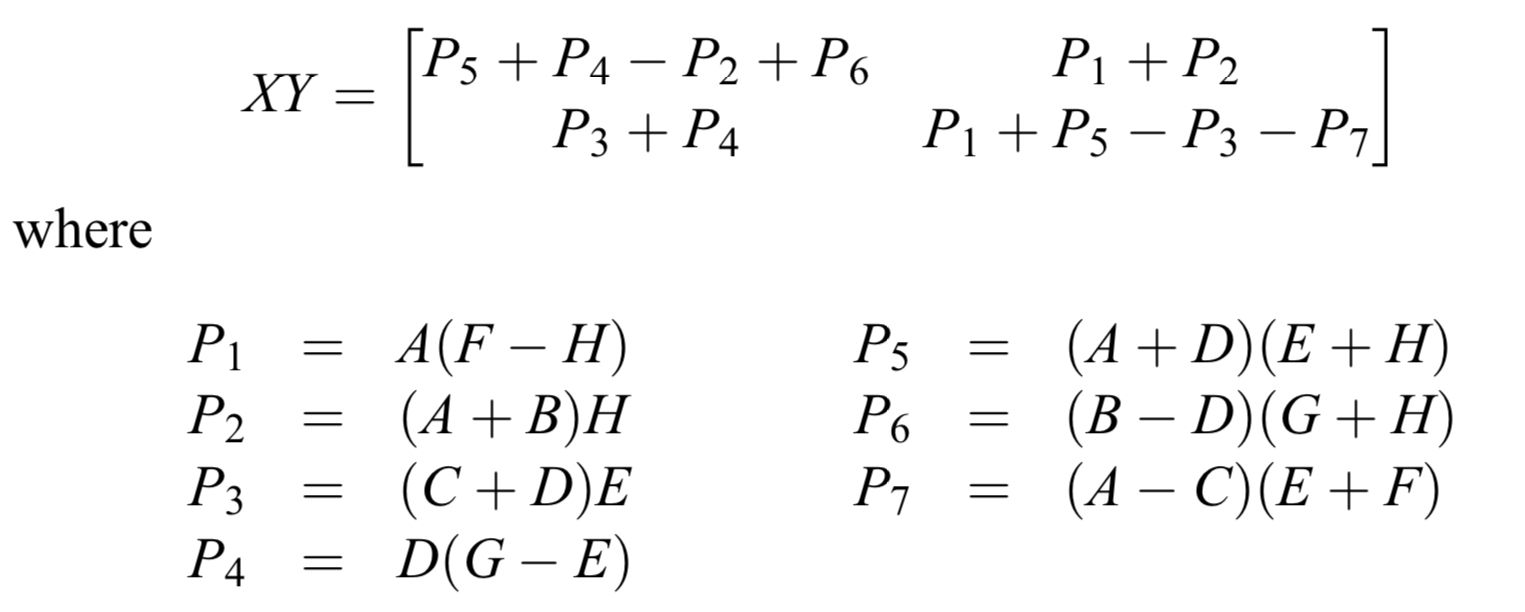
• $T(n) = 7T(n / 2) + O(n^2)$ → 复杂度 $O(n^{log_27}) \approx O(n^{2.81})$