1 活动安排问题(Interval Scheduling)
描述
- 任务 j 从 $s_j$ 开始,到 $f_j$ 结束
- 选出一个最大的不冲突的任务子集合
尝试
- 最早开始时间
- 最早结束时间 — correct
- 最短持续时间
- 最少冲突事件
算法

复杂度:O(nlogn)
- 先要对结束时间排序,需要O(nlogn)
- 遍历只需要O(n)
证明贪心算法的思路
- Counter — 反证
- Induction — 数学归纳法
- Nature — 分析问题的本质原理(高级)
证明该问题:反证法
- 假设该算法不能得到最优解
- 令 $i_1, \cdots, i_k$是贪心得到的结果,而 $j_1, \cdots, j_m$是一个最优解
- 并且假设这两个序列的前 r 项是相同的
- 由于贪心算法每次加入的都是结束时间最早的,因此 $f{i{r + 1}} \le f{j{r+1}}$
- 如果 $f{i{r + 1}} = f{j{r+1}}$,与“前 r 项相同”的假设冲突
- 如果 $f{i{r + 1}} < f{j{r+1}}$,那么可以用 $i{r+1}$ 把 $j{r+1}$ 替换掉,替换后仍然是最优解
- 综上,贪心得到的结果必是最优解
2 排课问题(Interval Partitioning)
描述
- 第 j 节课从 $s_j$ 开始,从 $f_j$结束
- 求最少需要多少个教室,能使得所有的课程不冲突
解法:每次考虑最早开始时间
算法

定义 depth:同一时刻下正在同时进行的课程数量记为 n ,depth 为 n 的最大值
复杂度:O(nlogn)
- 排序需要O(nlogn)
- depth 最小可能1,此时遍历共需要O(n)
- depth 最大可能为n ,此时遍历共需要O($n^2$)
- 如果使用优先级队列(堆)进行维护,则能够保证复杂度一直为O(nlogn)
- 对每个教室,以最晚结束时间进行维护,结束时间最早的放在堆顶
证明
- 前提条件1:需要的教室数量 $\ge$ depth
- 只需证明贪心算法得到的教室数 = depth
- 前提条件2:贪心算法不会让冲突的课程分在一个教室里
- 因此在分配第 d 个教室时,一定是因为有一个课程 j 与剩下 d - 1 个教室都冲突
- 因此在 $s_j + \epsilon$ 时刻,有 d 个课程正在同时进行
- 也就是说,当前分配到的教室数 = 当前的深度
- 因此,贪心策略得到的教室数量始终等于深度
3 最小迟交惩罚问题(Minimize lateness)
描述
- 任务 j 需要 $t_j$ 时间才能完成,并且需要在 $d_j$ 前做完
- 如果 j 在 $s_j$ 开始,那么它会在 $f_j = s_j + t_j$时结束
- 迟交惩罚记为 $l_j = \max {0, f_j - d_j}$
- 目标:如何规划,使得最大的迟交惩罚(lateness)达到最小
- 注意不是所有lateness的和!而是某一个lateness最大!
尝试
- 最短执行时间优先
- 最早ddl优先 — correct
- 最小slack的任务优先(Slack = $d_j - t_j$)
算法

复杂度:O(nlogn)
证明——数学归纳法
- 思路:Exchange property
首先,去掉idle time,使安排的任务是紧凑的
- 该操作不影响ddl,因此紧凑的安排方式与原来的解是等价的

定义inversion: $d_i < d_j$ 但是 j 排在 i 前面
贪心算法里没有inversion
交换inversion后,最大lateness不会增加,只会减少
证明:

假设交换前 lateness 的最大值为 $l_{max}$
交换后:
- 其他都不变
- $l_i’ \le l_i$,i 项减少
- $lj’ \le l_i \le l{max}$,j 项不增加
由以上推导,可以证明贪心算法是最优解
- 如果最优解无inversion,则贪心算法 = 最优解
- 如果最优解有inversion,交换后lateness有可能会减少,这说明该解不是最优解,矛盾
- 综上,贪心算法就是最优解
4 离线缓存问题(Offline caching)
描述
- cache 的容量为 k ,访问序列的长度为 m
- 序列已知 (offline)
- 如何规划使得 cache miss 的次数最少
最优解:farthest-in-future
- 换掉最远出现的值
- 不是online算法!因此LRU不是最优解!
证明:
首先,要求最优解只能在cache miss时进行替换
- 这里有个证明:可以将自由替换的解转化为只在miss时替换的解
道理很直观,形式化的证明很难想!
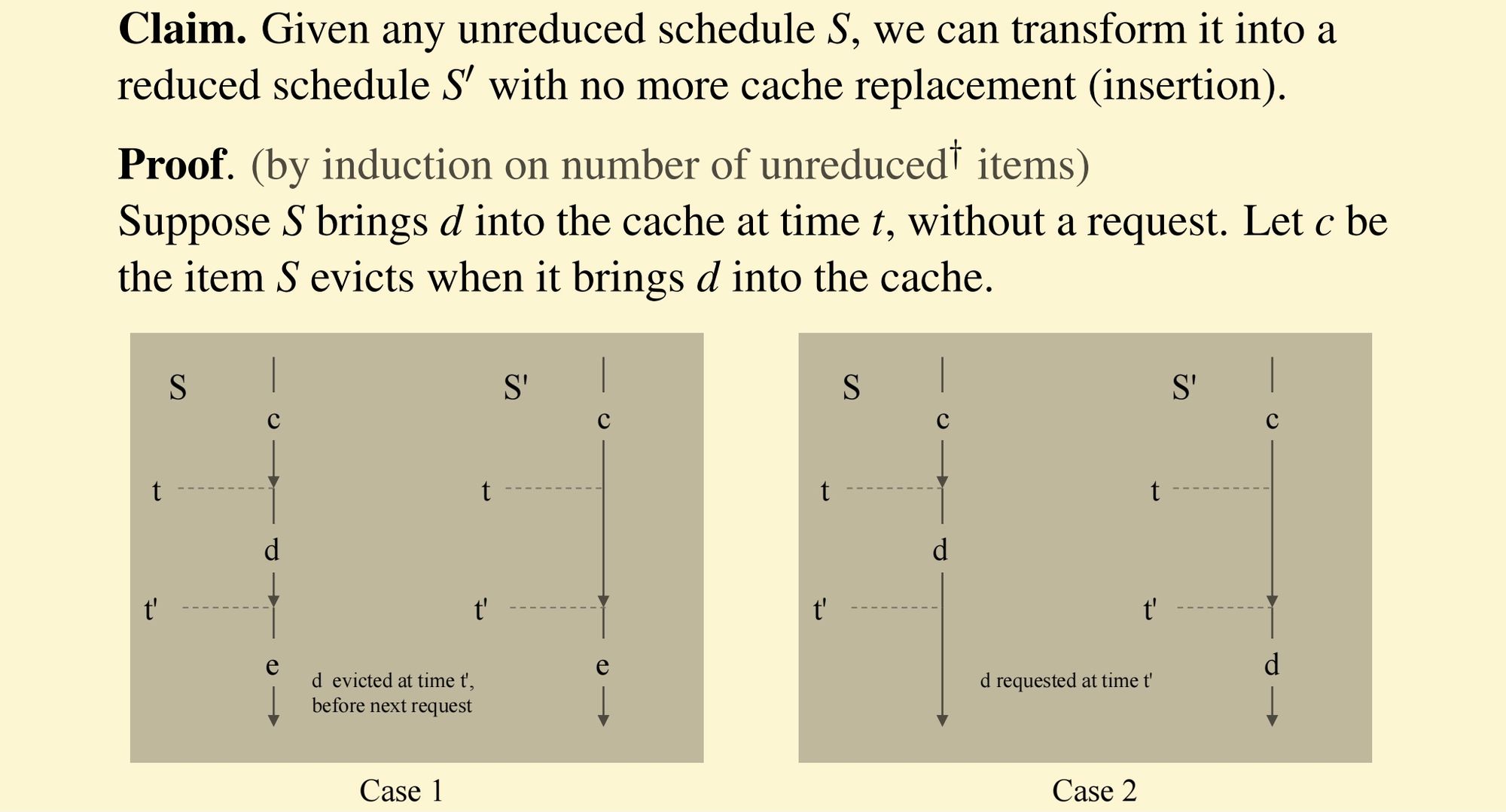
证明贪心算法为最优
- 数学归纳法
- 假设前 j 次贪心算法与最优算法相同,第 j + 1 次不同
- 证明最优算法的 cache 能够转化为与贪心算法的相同
- 请看PPT!
5 找零问题
- 使用最少的硬币数量表示给定的数值
- 策略:先换大的面值
- 证明:当小面值的数值和超过大面值的币时,将这些币换成更大的面值可以减少硬币数量
- 并不是所有的面值组合都能用贪心解决!