算法设计与分析 - 图算法

1 图探索

1.1 DFS

• 使用栈实现
• 时间复杂度：O(V + E)
• 使用 DFS 判断连通分量的数量
  • 每次调用 DFS 时，连通分量数 +1
• 括号定理
  • 把调用递归前的操作和递归结束后的操作看作一组括号
  • 递归过程中，不同对的括号只有包含和独立的关系，不存在相交
    • 只有 ( [ ] ) 和 ( ) [ ]，不存在 ( [ ) ]
    • 根据访问时间，记作 [pre number, post number]
• 先序遍历和后序遍历
• 边的类型
  • Tree edge：DFS 生成树的边
  • Forward edge：从一个结点指向非子结点的后代结点的边
  • Back edge：指向祖先的边
  • Cross edge：指向非祖先也非后代的已访问结点
• 有向无环图 Directed Acyclic Graph (DAG)
  • 如果有环，DFS的过程中会发现一个 back edge
  • 没有入度的结点称为 source
  • 没有出度的结点称为 sink
• 线性化、拓扑排序
• 强连通分量
  • 可以将强连通分量看作一个大的结点
  • 以这种方式，可以将任何图转化为有向无环图
• 如何寻找强连通分量
  • 引理
    • 从 sink 出发进行DFS，可以将sink对应的分量全部便利到
    • 最大的 post number 一定在 source 中
  • 先将图reverse，用 post number 找到 reverse之后的 source，即为原图的 sink
  • 从该 sink 出发可以找到对应的强连通分量
  • 把该分量记录下来并从原图中拿掉
  • 对剩下的图重复上述步骤，从而得到所有分量

1.2 BFS

• 使用队列实现

2 最短路

2.1 性质

• 任何最短路的子路径必须是最短路
• 图中有可能没有最短路
  • 例如图中有一个负权值的圈
• 最短路的三角不等式
  • 描述了可行解与最优解之间的关系
  • $d(v_1, v_2) \le d(v_1, v_3) + d(v_3, v_2)$

2.2 Dijkstra 算法

• 单源最短路
  • 注意区分于 Prim！那个是最小生成树！两者算法有点类似
  • 只能用于边权均为正的图
• 思路
  • 维护一个顶点的集合，该集合中所有的最短距离都是已知的
  • 每次从该集合外的顶点里选取一个距离源点 s 最近的顶点 v ，并加入到集合中
  • 更新顶点 v 所有邻居的距离
• 证明
  • 欣赏PPT即可
  • 先证明局部最优解 d[v] $\ge$ 最优解 d(s, v) → 反证法
  • 证明在算法结束的时候两者是相等的 → 反证法
• 对于无权图，Dijkstra 算法即为 BFS
• 补充：堆
  • 优先级队列一般用 heap 实现
  • binary heap
    • 以最小堆为例：父结点的值小于等于子结点的值
    • 插入：在最后增加一个结点，循环往上调 → O(logn)
    • 删除：删除根结点，把最后一个结点放在根结点，循环往下调 → O(logn)
    • 找最小：就是堆顶值 → O(1)
  • d-nary heap
    • 用 d 叉树实现
  • 二项堆 binomial heap
    • $b0$ 是一个点， $b{k}$ 由两个 $b_{k-1}$组成
    • 做 merge 时遵循二进制加法原则
    • 插入：就是做加法，加上一个 $b_0$
    • 删除最小：去掉根结点，把剩下的结点看作一个二项堆，与原二项堆合并
    • 删除某个结点：先调整到根结点，再删除
  • 斐波那契堆
    • lazy 版本的二项堆：先放进来，等到不满足了再调整
    • 双向循环链表链接根结点
    • 结点中有一个 mark，用于标记子结点是否被删除
    • 维护一个指向最小根结点的指针
    • 合并操作：将结点数量相同的堆合并起来（fibonacci）
    • 删除最小
      • 先做二项堆的操作：把去掉根结点以后的部分与
      • 如果头部的链表中有结点数相同的堆，则做一次合并
    • 将某个结点的值变小 / 变大

2.3 Bellman-Ford 算法

• 解决带负边权的单源最小路问题
• Dijkstra 不能解决负边权的原因
  • Dijkstra 认为每次都是局部最优解
  • 加入一个局部最小之后就不再改了
  • 但是后续有可能加入负边，加入后会比之前的局部最优解更小
• 解决思路：动态规划
  • 定义 OPT(i, v)：使用 i 条边得到的从 s 到 v 的最短路径
  • 考虑取第 i 条边和不取第 i 条边
  • $OPT(i, v) = \min { OPT(i - 1, v), \min{ OPT(i - 1, u) + w(u, v)} }$
  • 时间复杂度： $O(VE)$，空间复杂度： $O(V^2)$
• 优化 → Bellman-Ford
  • 只需要维护一个一维数组 M[v] 即可
  • 只有当前值 M[u] 更新时才去 check (u, v) 这条边
  • 空间复杂度降到 O(V)，时间复杂度最坏是 O(VE)，但实际更快
• 如果 OPT(n - 1, v) = OPT(n, v)，则没有负圈
• 如何找负圈
  • 添加一个结点 s 与所有其他结点相连，且边权均设为 0
  • 判断 OPT(n, u) 是否等于 OPT(n-1, u)，如果不等则有负圈

2.4 多源最短路

• 矩阵乘法思路

  • 动态规划思路
  • $d{ij}^{(m)} = \min_k{ d{ik}^{(m-1)} + a_{kj} }$
  • 类似于矩阵乘法： $c{ij} = \sum{k} a{ik} \cdot a{kj}$
  • 利用指数幂算法优化该乘法，可以将 $O(n^4)$ 降到 $O(n^3 \log n)$
  • 如果没有环，对于最后一次 n，有 $d{ij}^{(n-1)} = d{ij}^{(n)} = d_{ij}^{(n+1)} = \cdots$

• Floyd-Warshall 算法

  • 如果加入 k 后能使距离变小才加进去，否则不加
  • $c{ij}^{(k)} = min_k{ c{ij}^{(k-1)}, c{ik}^{(k-1)} + c{kj}^{(k-1)} }$
  • 时间复杂度： $O(n^3)$

• Johnson’s Algorithm

  • 思路：将边权 reweight，使得没有负值，从而能使用 dijkstra 算法

  • 定理：如果按照 $\hat{w} (u, v) = w(u,v) + h(u) - h(v)$的办法进行 reweight，则两个顶点间的任意路径的权值均相同

    

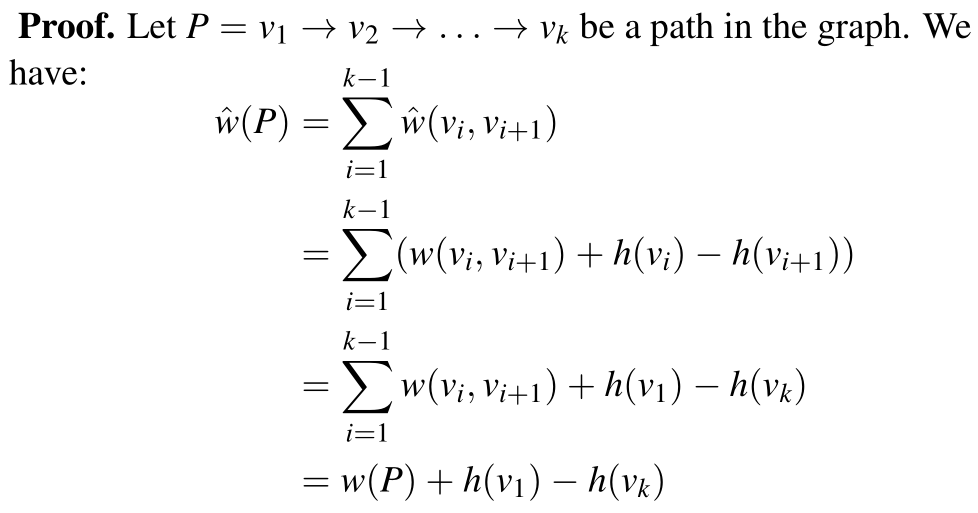
  • 算法流程

    • 新建一个顶点 s，并使其与所有顶点连通，新边赋权值为 0
    • 利用 Bellman-Ford 算法求得每个点到 s 的最短路，该值记为顶点的标号 $h(v)$
      • 还可以通过这种办法发现负圈
      • 时间复杂度 O(VE)
    • 用新的权值 $\hat{w}$ ，对每个顶点进行 dijkstra 算法
      • 此时的 $\hat{w}$ 为非负值
      • 时间复杂度 $O(VE + V^2 \log V)$
    • 将所有的 $\hat{w}$ 转化为原始的 w
      • 时间复杂度 $O(V^2)$

3 最大流

3.1 概念定义

• 最大流等价于最小割
• 定义流网络
  • 源点 s，终点 t
  • 从源点出发，每一个结点都可以被访问到
  • 每条边 e 都有一个容量 capacity = c(e)
• 定义分割
  • 将一个图 V 分割成两个子图 (A, B)，记作 s-t cut
  • 其中 $s \in A, t \in B$
  • 分割 (A, B) 的容量记作从 A 到 B 的所有容量之和
• 最小割问题：找到一个分割，使得该分割的容量最小
• 流的性质
  • 每条边上走过的流量 < 该条边的容量
  • 对于每个顶点（除源点和终点），进入的流量和出去的流量必须相同
• 定义流的值 = 所有从源点出去的流量 - 所有流入源点的流量

3.2 最大流与最小割

• 引理：一个流的值与任意一个分割 (A, B) 的 流量相同

  • $v(f) = \sum{\text{e out of A}} f(e) - \sum{\text{e in to A}} f(e)$

• 证明

  

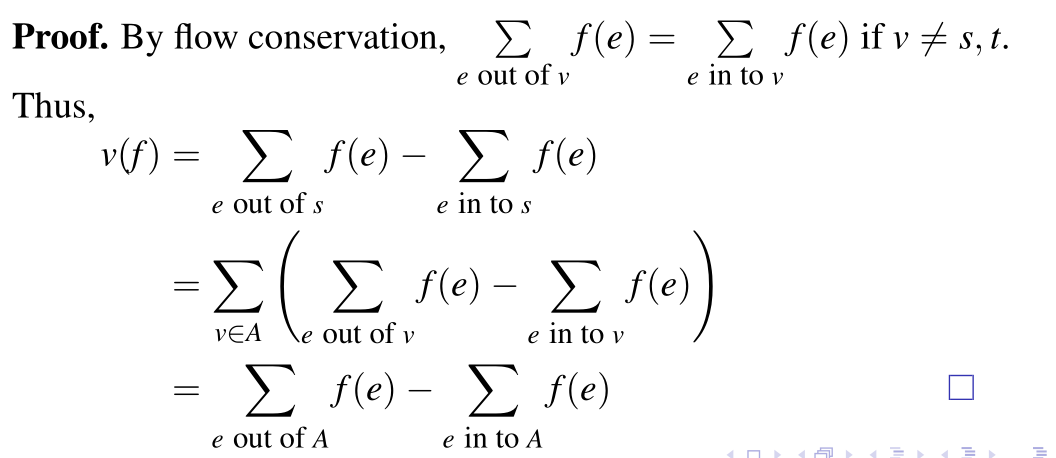
• 引理：对任意一个分割 (A, B)，流的值均小于该分割的容量，即 $v(f) \le cap(A, B)$

  • 证明：

    

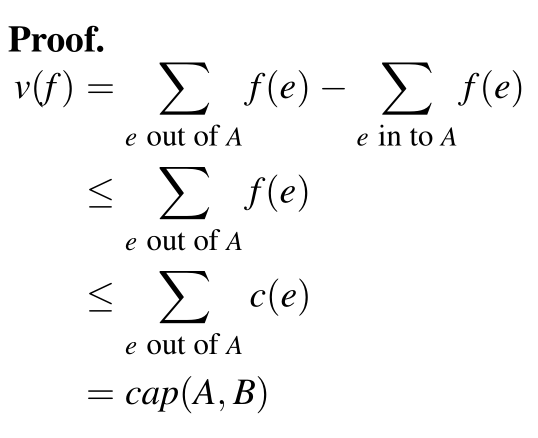
• 若 $v(f) = cap(A, B)$，则该流 f 为最大流，该分割 (A, B) 为最小割

3.3 Ford-Fulkerson 算法

• 尝试：贪心算法
  • 每次找到一条 s 到 t 的路径，添加该路径允许的最大流量
  • 重复找路径，直到不能再增加流量
• 贪心算法是不正确的！
  • 局部最优解 $\neq$ 全局最优解
  • 原因：每次用贪心在一条边上增加了流量后，该流量在后续不会被减少
  • 启发：需要找到一个办法，能够“撤回”不正确的流量
• 解决方案：剩余图
  • 每次记录一条路径后，增加一条反向边，用于后续撤回
  • 在正向边中，记录剩余的流量 $c(e) - f(e)$
  • 在反向边中，记录累计的流量 $f(e)$
• 增强路径 Augmenting Path
  • 如果该边是正向边，将当前路径的流量瓶颈累计在 f(e) 中
  • 如果该边是反向边，将该流量瓶颈从 f(e) 中减去
• 算法流程
  • 每次找一条增强路径，并更新图
  • 最终结果即是最大流
• 最大流 - 最小割理论：以下三个命题等价：
  • 存在一个分割 (A, B) 使 $v(f) = cap(A, B)$
  • f 为最大流
  • 对于 f 而言没有增强路径
• 复杂度分析（最大容量为 C）
  • 增强路径的数量 $\le E \times C$，因为每条增强路径至少增加了 1 点流量
  • 寻找一条增强路径（DFS 或 DFS） 需要 $O(V)$ 复杂度
  • 因此时间复杂度为 $O(VEC)$

3.3 优化

• 选增强路径的策略：选取足够大容量瓶颈的路径

  • 不一定要选最大的

• Capacity Scaling

  • 维护 scaling 参数 $\Delta$，初始值为大于等于容量 C 的最小的 2 的次幂
  • 令 $G_f(\Delta)$ 为边上的容量均大于 $\Delta$ 的子图
  • 在当前的子图中寻找所有的增强路径，并更新流量图
  • $\Delta = \Delta / 2$

• 复杂度分析

  • 外圈循环： $1 + \lceil \log_2 C \rceil$ 次

    • 每次对 $\Delta$ 除以 2

  • 每次循环中的最大流值不超过 $v(f) + m \Delta$

    • m 为顶点数量

      

  • 每次迭代中最多找 2m 个增强路径

    • 每个顶点来回找两次

  • 因此该算法的增强路径的总数为 $O(m \log C)$

  • 总的时间复杂度为$O(m^2 \log C)$