算法设计与分析 - 近似算法

• 推荐书籍： Computers and Intractability: A guide to the Theory of NP-Completeness
  • 附录整理了大部分 NP 问题以及规约方法

1 概念

• NP 优化问题 (NPO)

• 对于一个问题 P(I, sol, m, goal)

  • I：目标数据的集合
  • sol：可行解
  • m：评估函数
  • goal：最大问题 / 最小问题

• 近似比

  • $R(x, y) = \max{ \frac{m(x,y)}{opt(x)}, \frac{opt(x)}{m(x,y)} } > 1$

• F-APX

  • 该集合中的函数与函数 F 的近似比为常数
  • 例：log-APX

• PTAS (Polynomial Time Approximation Scheme)

• FPTAS

• 包含关系

  

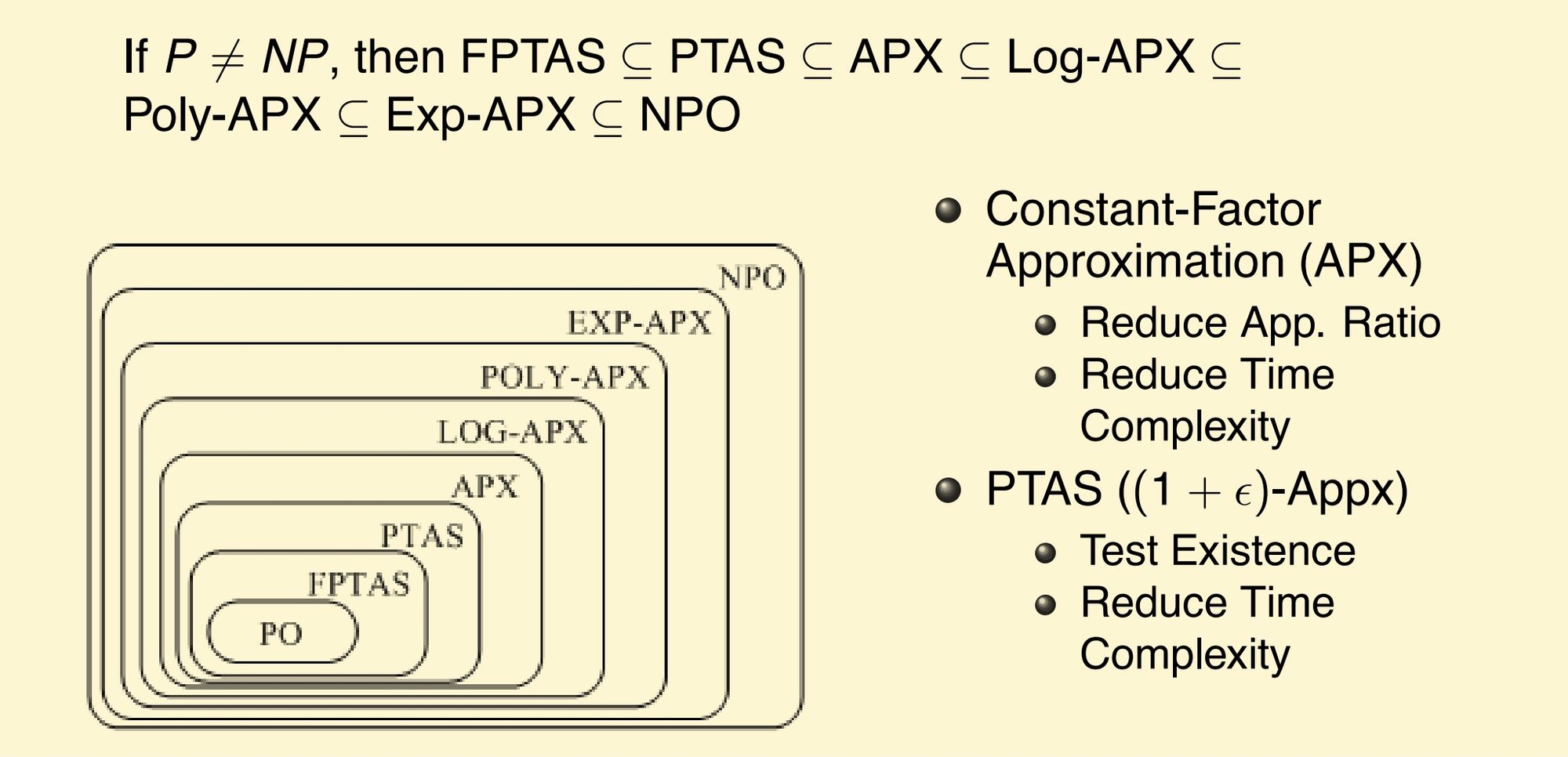
2 集覆盖问题 Set Cover Problem

• 在子集的序列中挑出一些子集，使得这些子集可以覆盖原集，并使得权重和最小

• 思路

  • 获得当前没被覆盖的 set 中权值最小的
  • 更新剩下的 price 为 $price(e) = \frac{c(S)}{|S-C|}$

• 时间复杂度：O(mn)

  • m 为 set 个数，n 为 element 个数

• 近似比：Log-APX

• Observation： $price(e_k) \le \frac{m^*(u)}{n-k+1}$

  • 最小值小于平均值

• Tight Example

  

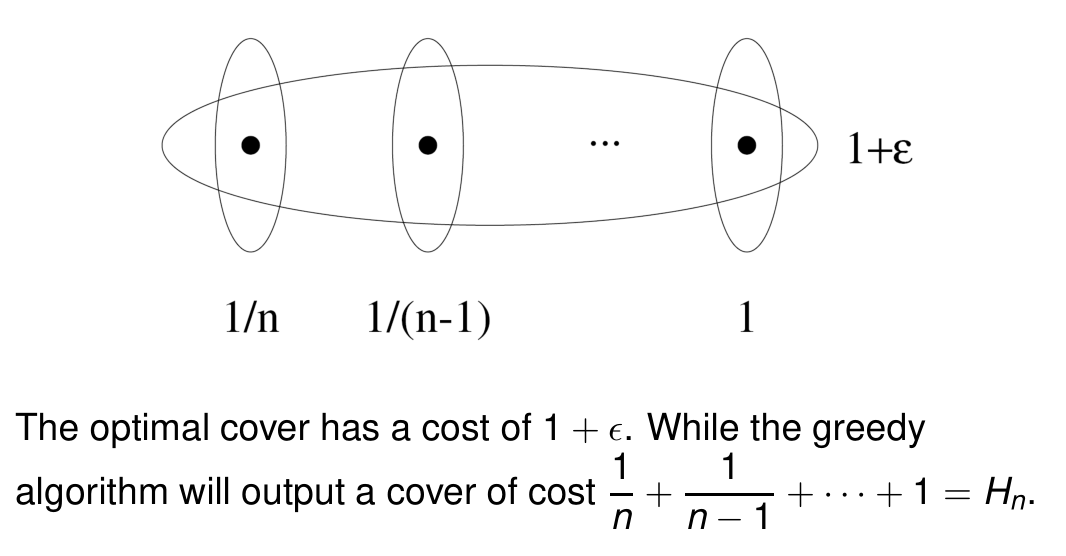
3 背包问题

• 取密度最大的

• 时间复杂度：O(nlogn)

• 近似比：可能任意坏

• Worst example

  

• 优化：对于贪心的结果和当前最大价值的物品，取两者中更大的那个

• 优化后近似比：2近似比

  • 最优解小于等于前半段 + 最后一个放不下的
  • 前半段小于等于算法解，因为算法还没做完
  • 最后一个小于 $p{max}$，而算法是取前半段和 $p{max}$ 的最大值
  • 故 OPT 小于等于 2 个最优解

4 顺序算法 (Sequential Algorithm)

• 即为贪婪算法

4.1 最大割问题

• 描述

  • 将一个集合划分成两个子集，使子集之间的边数最大

• 思路

  • 每次取一个点，判断该点与两个子集之间的边数量，把它放在边少的那个子集中

• 近似比：2

  • $A_{cut} \ge \frac{|E|}{2}$
  • $OPT \le |E|$
  • 因此 $\frac{OPT} {A_{cut}} \le 2$

• Tight example

  

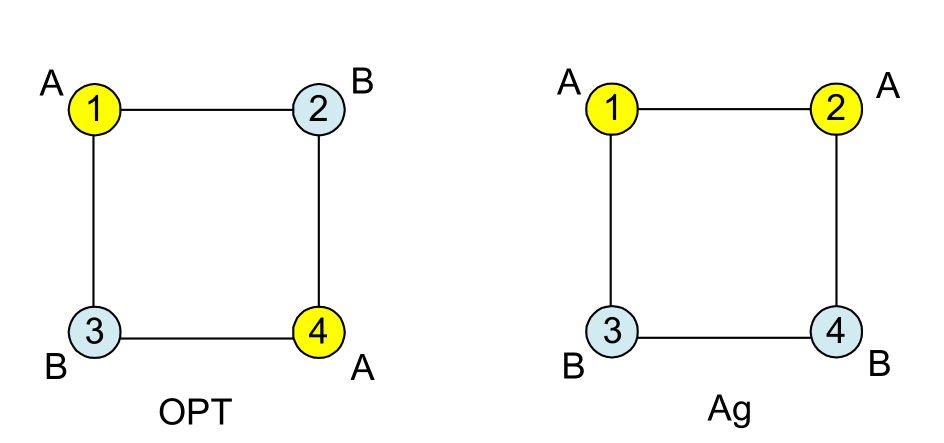
4.2 并行任务规划问题

• 描述
  • 有 p 个机器和一系列任务，需要将这些任务安排在机器上运行
  • 求这些机器所需的最大运行时间的最小值
• 思路
  • 按工作的长度降序排列
  • 每次迭代中，把当前工作放在已规划时间最短的机器上
• 近似比： $\frac{4}{3} - \frac{1}{3p}$

5 局部搜索 (Local Search)

• 只能在解的领域范围内找
• 在领域中找到一个比当前解更优的解

5.1 并行任务规划问题

• 思路

  • 先随便做一个规划

  • 找到最长的那个，看看能不能挪到其他地方去，挪不了就停止

    

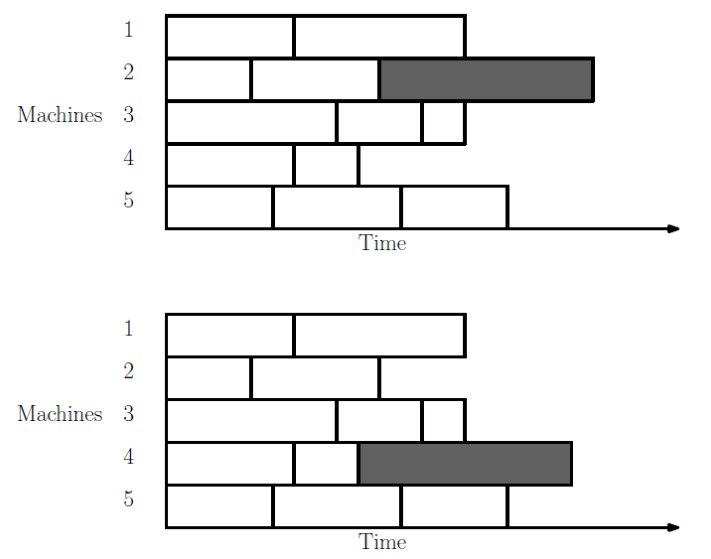
• 时间复杂度：O(n)

  • 每个任务只会挪一次

• 近似比：2

5.2 最大割问题

• 先列出所有可行解
• 找到可行解中最好的那个
• 近似比：2

6 线性规划舍入算法 (LP Rounding)