GAMES202 - Environment Lighting


    
  1. 1. 1 概念
  2. 2. 2 Image-Based Lighting (IBL)
    1. 2.1. 2.1 Lighting 项
    2. 2.2. 2.2 BRDF项
  3. 3. 3 环境光阴影
  4. 4. 4 频率相关概念
  5. 5. 5 球谐函数(Spherical Harmonics, SH)
    1. 5.1. 5.1 基本概念
    2. 5.2. 5.2 用球谐函数处理环境光
  6. 6. 6 Precomputed Radiance Transfer (PRT)
    1. 6.1. 6.1 基本概念
    2. 6.2. 6.2 Diffuse
    3. 6.3. 6.3 Glossy
    4. 6.4. 6.4 复杂度
    5. 6.5. 6.5 多次bounce、焦散(Caustics)现象
  7. 7. 7 Wavelet 小波函数

1 概念

  • 用一张图来记录在场景中往任意方向看，可以看到的光照
  • 认为光照来自于无限远
  • 储存方式
    • Spherical Map
    • Cube Map
  • 仍然需要对渲染方程进行求解
  • 对于环境光问题，近似求解渲染方程的办法：
    • Image-Based Lighting (IBL)
    • Precomputed Radiance Transfer (PRT)

2 Image-Based Lighting (IBL)

  • 通用解法：蒙特卡洛积分 → 慢！

如果 shader 里出现了采样，一般认为是无法用在实时渲染中的； 但由于最近降噪方法的兴起，一部分采样算法能在实时渲染中使用了

  • 使用之前的重要近似方案

    • 如果 BRDF 是 glossy 的，那么有效的积分域将会很小；

    • 如果 BRDF 是 diffuse 的，那么它的函数值变化是非常smooth的

      img

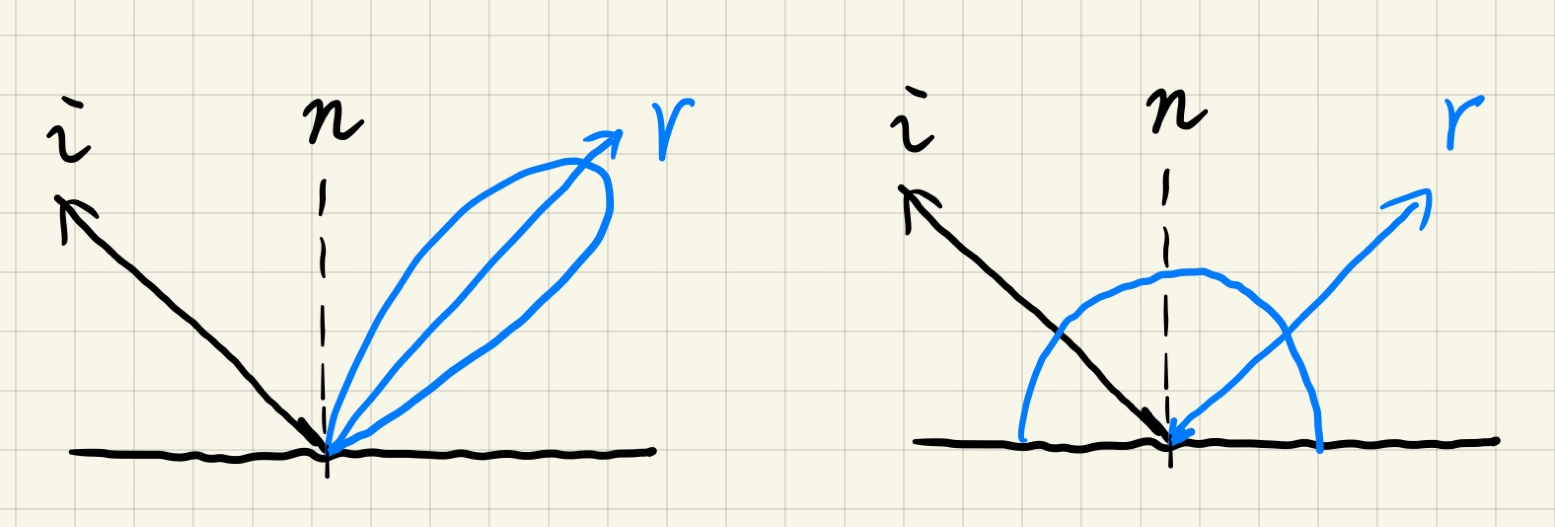
  • 回顾重要近似

    img

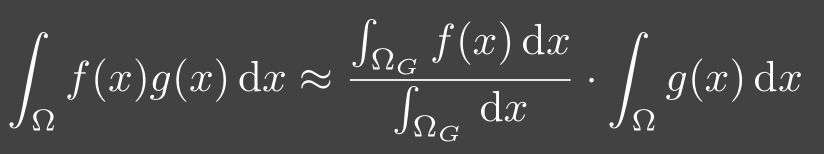
  • 工业界把这种拆分方法叫做 Split Sum

    img

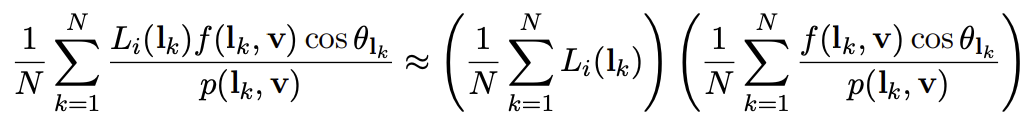
2.1 Lighting 项

  • 把渲染方程的 lighting 项拆出来

    img

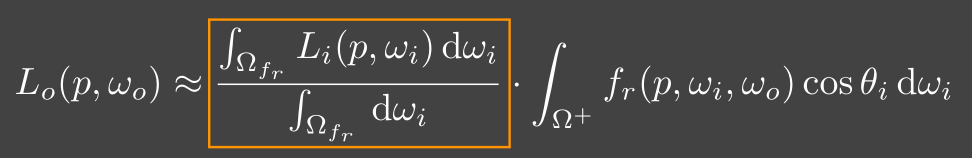
    • 相当于先对环境光贴图做滤波操作，再乘到最后的结果中

  • 可以预先对环境光贴图做滤波，不需要在渲染的过程中做！

    • 类似于Mipmap

  • 上面的操作称为prefiltering

    • prefiltering + 单次查询 = 不做滤波 + 多次查询
    • 通过预计算，降低了开销

2.2 BRDF项

回顾Microfacet BRDF：

$f(i,o) = \frac{F(i,h) \cdot G(i,o,h) \cdot D(h)}{4 (n,i)(n,o)}$，h → 入射向量与反射向量的中值

F → 菲涅尔项，G → shadow masking，D → 微表面法线分布 对菲涅尔项进行近似：

$R(\theta) = R_0 + (1 - R_0)(1 - \cos \theta)^5$, $R_0 = (\frac{n_1-n_2}{n_1+n_2})^2$

  • 仍然考虑预计算的方法
  • 降低参数空间的维度
  • 菲涅尔项可以拆成只用 $R_0$ 和 $\theta$ 表示的形式

img

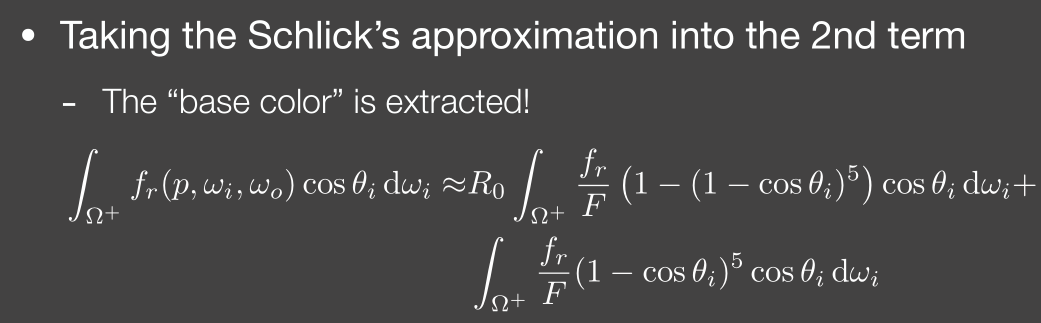
  • 积分值可以预先计算出来，作为一张二维纹理

    img

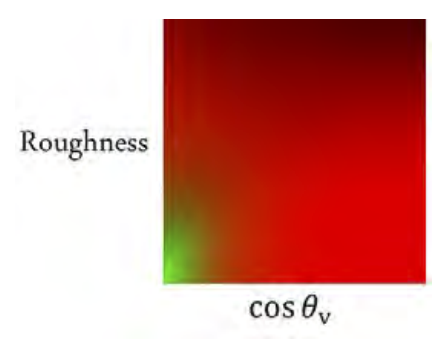
  • 每一个 BRDF 对应了一张确定的表，与场景中的光线分布无关

3 环境光阴影

  • 实时渲染下，得到环境光阴影是非常困难的
  • 从不同的角度看这个问题
    • 看做一个多光源问题
      • Shadow map的数量与光源数量成线性关系
    • 看做一个采样问题
      • Visibility项异常复杂，并不能简单地从环境光中分离出来
  • 目前的解决方案
    • 只考虑最亮的光源生成的阴影
  • 前沿研究
    • Imperfect shadow maps
    • Light cuts
    • RTRT (Real-Time Ray Tracing)
    • Precomputed Radiance Transfer(PRT)

4 频率相关概念

  • 频率
    • 任何一个乘积的积分都可以看做一个滤波
      • $\int_{\Omega} f(x)g(x) dx$
    • 低频 = smooth / 变换比较小
    • 积分结果的频率会比任意一个单独函数的频率都低
  • 基函数
    • 可以用基函数的不同组合来描述不同的函数
    • 例：傅立叶级数、泰勒级数

5 球谐函数(Spherical Harmonics, SH)

5.1 基本概念

  • 是一系列的、定义在球面上的、二维的一组基函数

  • 可以将一个二维函数 $f(\omega)$ 分解成一组球谐函数的和

  • 类比于1维的傅里叶级数

    img

  • 每一行的频率 l 都是一样的，l 越大，频率越高

  • 每个频率下有 (2l + 1) 个不同形状的基函数

  • 每个基函数都有一个编号，对于第 l 行，编号的范围为 [-l, l]

  • 前 n 阶总共有 $n^2$个基函数

  • 每个基函数是用 Legendre 多项式来描述的

  • 计算球谐函数的系数

    • 求系数的过程被称为投影
    • $ci = \int{\Omega} f(\omega)B_i(\omega)d\omega$

  • 性质

    • 正交性
    • 投影 / 重构很好计算
      • $ci = \int{\Omega} f(\omega)B_i(\omega)d\omega$
    • 旋转很好计算
      • 旋转原图 → 旋转所有的基函数
      • 旋转任一个基函数后，都可以用同阶的基函数的一个线性组合来描述
    • 卷积很好计算
    • 可以用前几阶的基函数表示低频区域

5.2 用球谐函数处理环境光

  • Diffuse BRDF表现起来像一个低通滤波器
  • 一般情况下，用 3 阶球谐函数就能基本上拟合Diffuse BRDF
  • 既然经过Diffuse物体后只剩下低频部分，那我们何不在描述光照时也只使用低频部分呢？
  • 使用球谐函数来描述环境光
    • 只要材质是Diffuse，用 3 阶 SH 就能达到非常准确的近似结果
  • 把积分过程转化成了函数相乘，使得渲染方程实际可解
  • 环境光贴图中有 Spherical Map
    • 可以将该贴图分解为 3 阶的 SH 函数，并用在 shading 中，得到准确的环境光结果
  • SH适合做低频的拟合，对高频部分的拟合效果不够好

6 Precomputed Radiance Transfer (PRT)

6.1 基本概念

  • Lighting项、Visibility项、BRDF项均可以描述为球面函数

  • 思路

    img

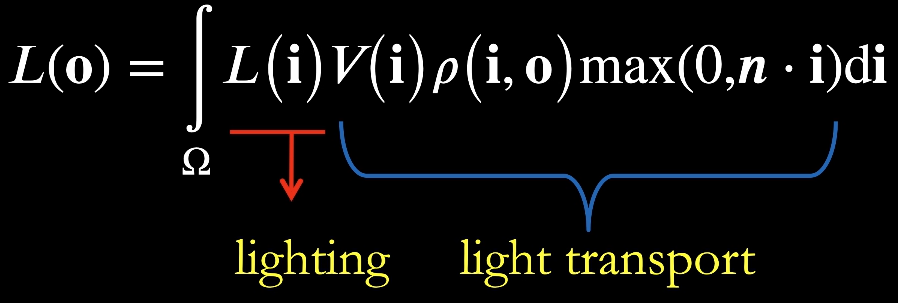
    • 把 Lighting 项拆成基函数
    • 把除了 Lighting 项的部分称为 Light transport 项
    • 假设只有 Lighting 是变化的，Light transport 对于每一个 shading point 而言都是不变的
    • 可以把Light transport看成 shading point 的一个属性
    • 因此可以在渲染之前，把Light transport预先计算好

  • 缺点

    • 预计算意味着场景中的物体是不能动的，如果动了就要重新算
      • 但是光源可以是动态的（由 SH 易于旋转得到）
    • 需要存储大量的预计算内容
    • 由于SH函数的性质，只适合低频的环境光，不适合高频

  • 注意：Visibility项与光照无关！

    • Visibility项是从相机出发，判断shading point的位置是否被其他物体遮挡，与光照分布无关
    • 之前Shadow Map方法只是利用光照条件来快速得到Visibility项的值

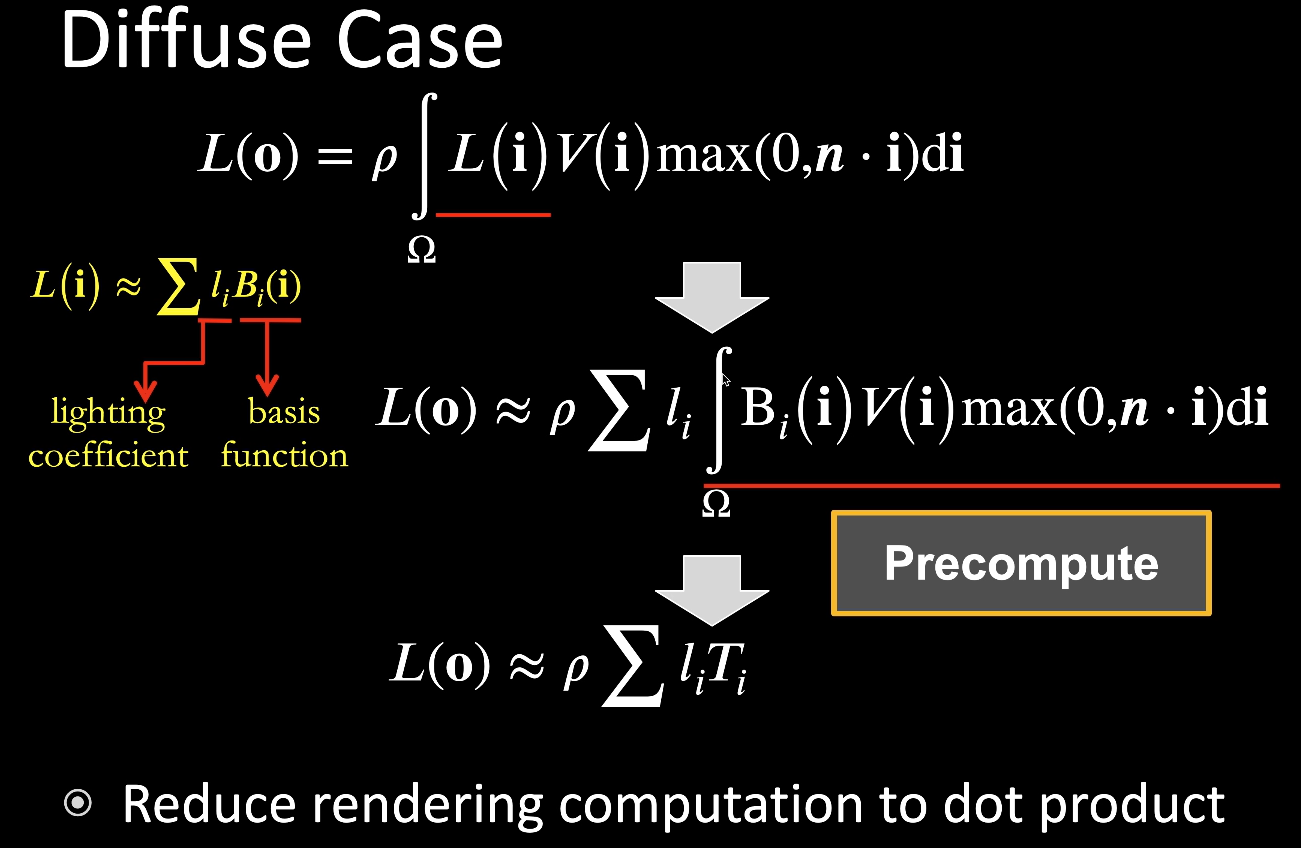
6.2 Diffuse

  • BRDF是常数，可以提出来放到积分前面

  • 预计算内容：Light transport投影到基函数上的系数

  • 一种理解方式

    • 对系数的预计算相当于以基函数作为光源，求出得到的光照结果

    • 实际光源相当于基函数的一个线性组合

    • 因此实际的环境光照结果相当于预计算结果的一个线性组合

      img

  • 另一个理解

    • 直接把 light transport 也拆成基函数

      img

    • 由于SH函数的正交性，不同的基函数结果为 0 ，因此仍然会得到与之前的理解相同的结果

6.3 Glossy

img

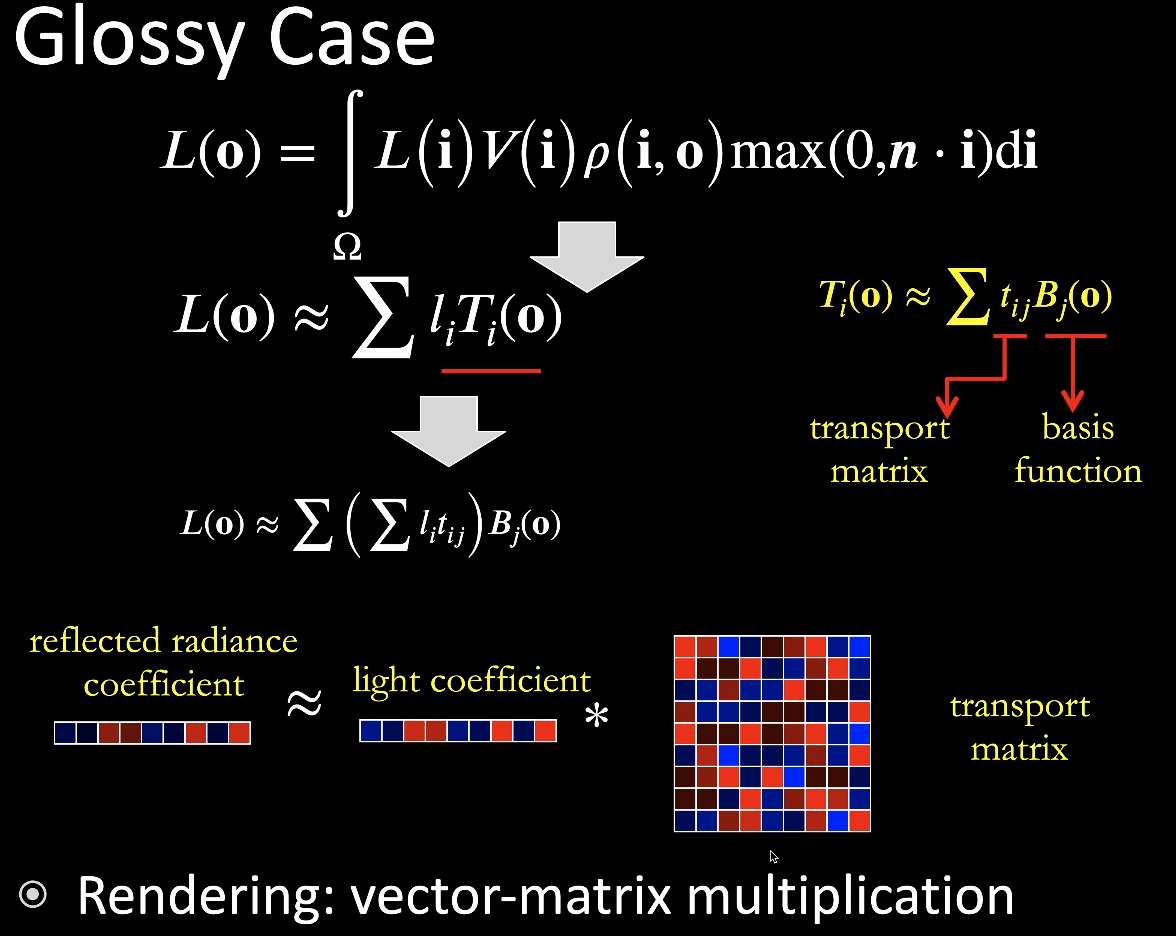
  • Glossy结果与观察视角有关 → Light transport 投影到基函数之后，仍然是 o 的函数
  • 将投影后的系数再向 o 空间的基函数投影
  • 代价
    • 每一个顶点处都需要存储一个矩阵，引入了大量存储空间
    • 运算时需要做矩阵乘法
  • 缺点
    • 如果 glossy 非常高频，接近镜面反射，SH函数的拟合效果会不太好
    • 因为SH对低频部分的拟合比较好，如果要拟合高频部分需要用非常高阶的SH函数

6.4 复杂度

  • 一般情况下，使用 4 阶 16 个 SH 函数
  • Diffuse：对于每个顶点，对长度为 16 的向量进行点乘
  • Glossy：对于每个顶点，计算长度为 16 的向量和 16x16 矩阵的乘积

6.5 多次bounce、焦散(Caustics)现象

  • 光线传输的正则表达式
    • L = Light, E = Eye, G = Glossy, D = Diffuse, S = Specular
    • 光线直接进入眼睛：LE
    • 光线弹1次进入眼睛：LGE
    • 光线弹若干次进入眼睛：L(D|G)*E
    • 焦散（光线先打到光滑的容器内壁，再进行反射）：LS*(D|G)*E
  • 无论light transport有多复杂，只要预先计算好，渲染时的运行时间将会与transport部分无关
  • 预计算结果可以采用离线渲染办法得到 (Path tracing等)

7 Wavelet 小波函数

  • 也是一组基函数

  • 定义在图像块上

  • 这里展示的是二维的 Haar 小波

    img

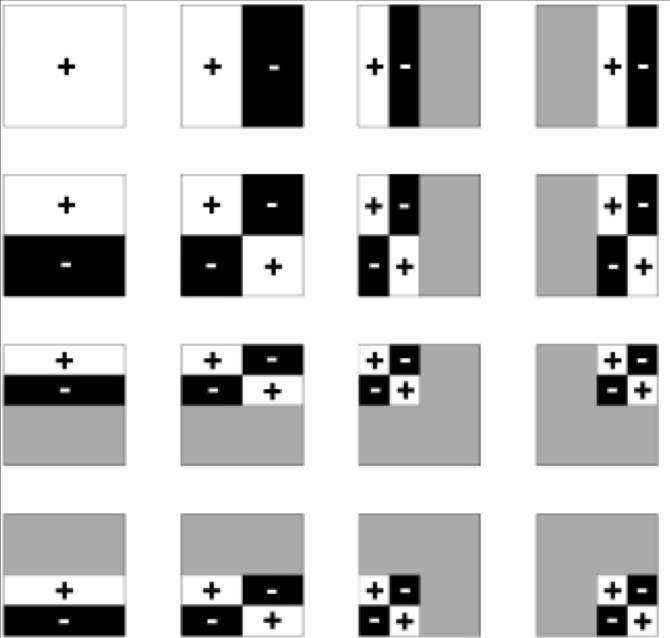
  • 不同的小波函数的定义域不同

  • 投影到小波函数上之后，有大量的系数接近 0

  • 是一个非线性的近似

  • 优点：支持全频率的表示

  • 缺点：不支持快速的环境光旋转

扫一扫，分享到微信

微信分享二维码

    缺失模块。
    1、请确保node版本大于6.2
    2、在博客根目录（注意不是yilia根目录）执行以下命令：
    npm i hexo-generator-json-content --save

    3、在根目录_config.yml里添加配置： 

      jsonContent:
    meta: false
    pages: false
    posts:
      title: true
      date: true
      path: true
      text: false
      raw: false
      content: false
      slug: false
      updated: false
      comments: false
      link: false
      permalink: false
      excerpt: false
      categories: false
      tags: true