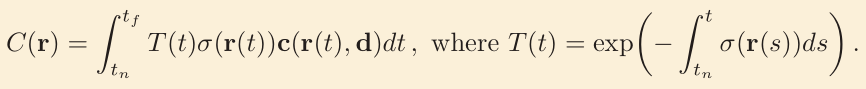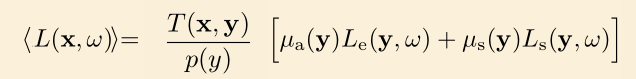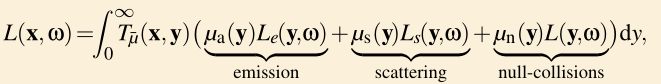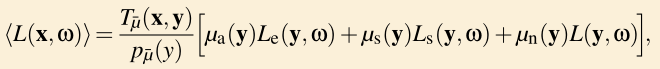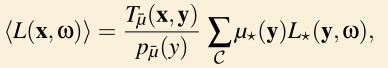Monte Carlo Volume Rendering 原理

原理

参考资料

• Transmittance 计算，https://zhuanlan.zhihu.com/p/519969318
• delta tracking，https://zhuanlan.zhihu.com/p/166116224
• volume rendering siggraph18 课程，https://cs.dartmouth.edu/wjarosz/publications/novak18monte-sig.html
• volume rendering survey, https://cs.dartmouth.edu/wjarosz/publications/novak18monte.pdf

公式

• nerf 的积分公式
  • 
• 目标：获得一个数值解，使得该数值解的期望值等于积分的值
  • nerf ray marching：采样 1 条光线，这条光线上取 1024个 采样点
  • monte-carlo：采样 n 条光线，每条光线上取 少量 采样点，最终结果为 n 条光线结果的均值
    • 每条光线相互独立，因此可以每一帧只采样 1 条光线，再根据相邻帧的结果进行降噪（即时序降噪）
  • 每像素采样数 (spp) = 采样光线的数量
• 完整的 volume rendering 公式
  • 记号说明：密度 $\sigma \to \mu$，颜色 $c \to L$，$\tau = \int_0^y\mu_t(s) \,\mathrm{d}s$
  • nerf 没有 in-scattering 这一项
  • 
• 利用下式写成蒙特卡洛形式 $$\int_a^bf(x) \,\mathrm{d}x \to \frac{1}{N}\sum_{i=1}^N \frac{f(x_i)}{p(x_i)}$$
  • 

Distance Sampling

• 目标：利用概率密度函数，把 $T$ 消掉
• 由于 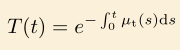, $T \in [0, 1]$，在 $[0, +\infty)$ 上单调递减
• 取 $F(t) = 1 - T(t)$ 作为累积密度函数 (CDF)
  • 此时 $p(t)$ 正好为 $\mu \cdot T$
• 
• 采样时，先取一个 $[0, 1]$ 之间的随机数 $\xi$，令 $F(t) = \xi$，解出 $t$ 的值作为采样点的位置
• 如果 $\mu_t$ 是常数，可以直接得到 $F^{-1}$ 的解析式
• 

Null Collision

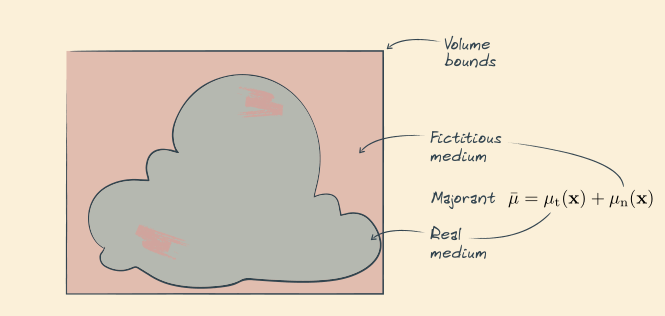
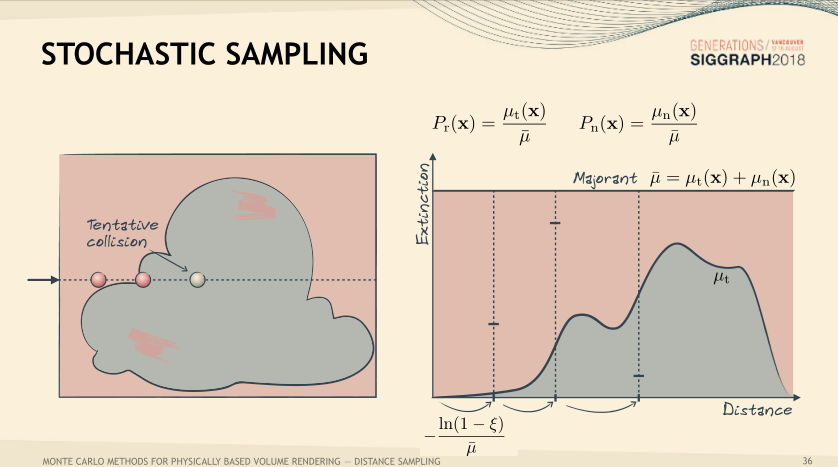
• 目标：想办法把空间填充成均匀的
• 向空间中填入虚拟粒子（粉色），与真实粒子（灰色）构成一个均匀的空间

• 虚拟粒子不影响光线原本的传播

  • 

• 例子：采样一条光线

  • 每次前进 $-\frac{\ln (1-\xi)}{\bar\mu}$
  • 如果采样到虚拟粒子，认为是一个 null collision，继续向前取采样点
  • 如果采样到真实粒子，认为光线被该粒子挡住，停止向前
  • 

• 积分公式

  • 

• 蒙特卡洛形式

  • 

  • 

• $L_*$ 用俄罗斯轮盘赌的方法估计，即

  $$\langle L_*(y, \omega) \rangle = \left\{ \begin{matrix} \frac{L_*(y)}{P_*(y)}&, \xi < P_*(y)\\0&,\mathrm{otherwise}\end{matrix} \right. \\$$

• 因此

  $$\langle L(x, \omega) \rangle = \sum_C^{ \;} w_*(x)L_*(y, \omega)\\$$

  其中

  $$w_*(x) = \frac{T_{\bar\mu}(x, y)}{p_{\bar\mu}}\frac{\mu_*(x)}{P_*(x)}\\$$

• 由于

  $$p_{\bar\mu} = \bar\mu \cdot T_{\bar\mu}(x, y)\\$$

  故

  $$w_*(x) = \frac{1}{\bar\mu}\frac{\mu_*(x)}{P_*(x)} = 1\\$$