红黑树是一种自平衡二叉搜索树。由于其良好的特性，红黑树被广泛应用于许多地方，例如C++的STL容器以及Linux的非实时任务调度。本文将对红黑树的原理和各种操作算法进行分析。

1 定义

红黑树的示意图如下：

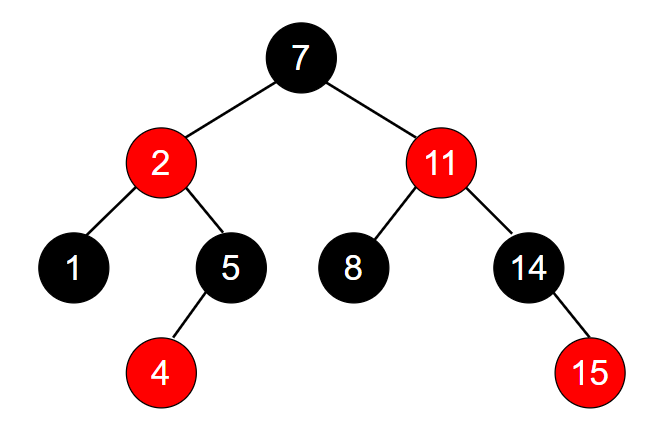
首先，红黑树必须是一棵二叉搜索树。同时，红黑树必须满足以下5条性质：

• 性质1：每个结点要么是黑色的，要么是红色的；

• 性质2：根节点必须是黑色的；

• 性质3：每个“叶子结点”都是黑色的；

  容易混淆的是，这里的“叶子结点”并不是我们通常理解的叶结点，而是指空指针结点NIL，所以我们在很多文章中看到的红黑树是下面这个样子的：

  

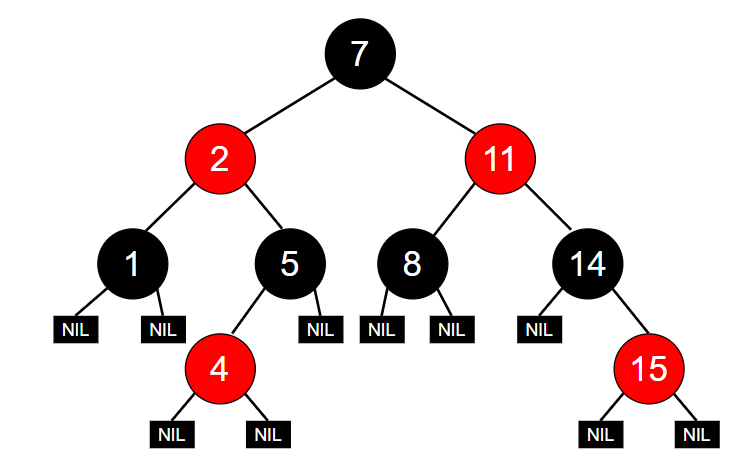
  Tips: 个人认为，把NIL结点看做叶子结点非常容易把自己搞晕。。所以这条性质可以理解为这样：如果一个结点的某个子树为空，则假设这个空子树的位置有一个黑色的结点。在后面的红黑树操作分析中，我们可以更好地理解这一条性质。

• 性质4：如果一个结点是红色的，那么它的两个子结点必须是黑色的；

  推论：1. 从任一结点到叶结点的路径上不能出现两个连续的红色结点；2. 红色结点的父结点必须是黑色的。

• 性质5：对于每个结点，从该结点到子树上叶结点的任意一条路径上，经过的黑色结点数量相同。

  这条性质是红黑树最重要的性质，它确保了红黑树中任意一条路径的长度都不会超过其他路径长度的两倍。因此，红黑树是一棵相对接近平衡的二叉树，性能较好。

  为了保持这5条性质，我们在插入和删除等操作中需要对红黑树的结构进行相应的调整。

推荐大家看看这个知乎回答：为什么这么多关于红黑树的面试题呢？ - 敖丙的回答 - 知乎 https://www.zhihu.com/question/312327402/answer/1560653215

这位大佬比较硬核地解释了红黑树的一些原理，包括2-3-4树模型和红黑树的联系等，看完后会对红黑树有更深的理解！

2 查找 / 搜索

红黑树是一棵二叉搜索树，因此查找操作和普通的二叉搜索树类似，流程如下：

1
2
3
4
5
6
7
8
9

// 搜索值为val的结点
当前结点 = 根结点
if(val == 当前结点值) {
    返回当前结点
} else if(val < 当前结点值) {
    在左子树中递归寻找
} else {
    在右子树中递归寻找
}

3 旋转

在之后对红黑树的结构调整操作中，我们可能需要对某两个结点进行旋转操作，以调节它们的上下关系，使左右子树相对平衡。例如，下面是对结点2进行左旋操作的示意图。注意结点2和结点4的上下关系：

最近在读第5版的《C++ Primer》，发现C++11标准中有很多非常实用的新特性。这里简单总结下C++11标准中处理变量类型的一些特性。

1 类型别名

1.1 typedef

typedef关键字在C++11之前就可以使用，作用是定义一个类型的别名，换句话说，它是某种类型的同义词。例如：

1

typedef double wages;  // wages是double的同义词

这样wages就成为了double的一个别名。只要是类型名能出现的地方，就能够使用类型的别名：

1
2

double a = 1.2;
wages b = 2.3;

typedef在给指针起别名的时候会遇到一些容易混淆的地方。

1.1.1 与宏定义的区别

下面的代码将pstring作为char*类型的别名，并定义一个常指针变量cstr：

1
2

typedef char *pstring;
const pstring cstr = nullptr;

因此变量cstr的数据类型为const pstring，意味着该指针是常量，不能修改指针所指的位置，但是可以通过该指针修改指针指向的字符内容。

类似地，如果使用宏定义来声明pstring，即：

1
2

#define pstring char*
const pstring cstr = nullptr;

由于在编译预处理过程中，代码中的pstring文本会被替换为char*，因此这段代码等价于：

1

const char* cstr = nullptr;

也就是说，这样定义出来的变量cstr为指向const char数据类型的指针，即指针所指的位置可以修改，但是不可以通过该指针修改指向的字符内容。

1.1.2 函数指针的别名

typedef最容易用错的时候是在给复杂的数据类型命名时，比如函数指针。例如我们要为下面这个函数的函数指针起一个别名pfunc：

单元测试是项目中非常重要的一个环节。在开发的过程中，应该养成每实现一个小模块就相应地做一系列单元测试的习惯，以保证该模块的正确性。这篇文章将简单介绍GTest框架以及如何利用CMake为自己的项目添加单元测试模块。

运行环境

Windows + gcc 4.9.2 + GNUWin32，使用VS Code的CMake Tools插件

1 CMake集成的测试工具——CTest

要使用CTest，用户需要先写一份测试代码。通常我们会使用一些测试框架来辅助我们进行测试（如下面的GTest），但这里我们先用最原始的方式，即在代码中使用assert()语句来判断结果的正确性，类似下面这样：

1
2
3
4
5
6
7

// test.cpp
#include <cassert>
int main() {
    assert(2 * 3 == 6);  // true
    assert(2 * 3 == 5);  // false
    assert( /* Expression */ )
}

使用assert()的目的是当测试结果不正确时，测试程序会终止，从而能被CTest检测到该测试程序是否正常结束。

在CMakeLists.txt文件中，首先将我们设计的功能代码添加为库文件，例如，

1

add_library(hello_lib hello.cpp)

之后，开启CTest测试模块，

1

enable_testing()

然后添加一个用于测试的可执行文件，并将需要测试的库文件链接到该可执行文件上，

1
2
3
4

add_executable(hello_test test.cpp)
target_link_libraries(hello_test
    hello_lib
)

最后，使用add_test()函数为CTest添加一个测试项，

1

add_test(test1 hello_test)

add_test()函数的参数形式可以更加复杂，详细可以参阅CMake的官方文档。这里是一种简单用法，第一个参数是该测试项的名字，第二个参数是该测试项对应的可执行文件的名字。因为这两个参数指代的对象不同，所以即便它们像下面这样名称相同，CMake也不会报错：

1

add_test(hello_test hello_test)

之后建立build目录并构建CMake项目。这里我使用了VS Code的CMake Tools插件帮我完成了这个步骤。

进入build目录，输入make test命令，就能看到CTest的测试结果。测试通过时输出如下所示：

1
2
3
4
5
6
7
8
9
10
11

D:/example/build> make test
Running tests...
Test project D:/example/build
    Start 1: Test1
1/2 Test #1: Test1 ............................   Passed    0.42 sec
    Start 2: Test2
2/2 Test #2: Test2 ............................   Passed    0.36 sec

100% tests passed, 0 tests failed out of 2

Total Test time (real) =   0.82 sec

2 GTest——GoogleTest

GoogleTest是Google的开源C++单元测试框架，主要有GTest和GMock两个功能模块。这里简单介绍一下GTest模块的基本用法，GMock模块等以后有机会使用的时候再来研究。

2.1 集成GTest到项目中

一般通过以下两种方式可以比较优雅地将GTest集成到项目中：

对github项目https://github.com/ttroy50/cmake-examples.git 进行学习总结

运行环境

Windows + gcc 4.9.2 + GNUWin32，使用VS Code的CMake Tools插件

1 Out-of-Source Build

在构建CMake项目时，一个非常重要的原则是：不要把构建后生成的文件和源代码混在一起！

一般采取的做法是在项目根目录下新建一个build目录，然后在build目录中构建Cmake项目。这样如果需要重新构建项目，只需要把build目录删掉再重新构建即可，不会污染原项目的文件结构。

CMake命令如下：

1
2
3
4

mkdir build
cd build
cmake ..    # 构建CMake项目，生成Makefile文件
make        # 根据Makefile文件生成可执行文件

由于我使用gcc编译并且安装了GNUWin32，因此可以使用make命令生成可执行文件。一般在Windows环境下会默认使用Visual Studio的编译器，这样在执行cmake .. 命令后会生成.sln后缀的VS项目，使用Visual Studio打开并构建工程即可。

2 最简单的情况 —— Hello CMake

如果我们整个工程里面只有一个源文件main.cpp，CMake文件只需要三行即可：